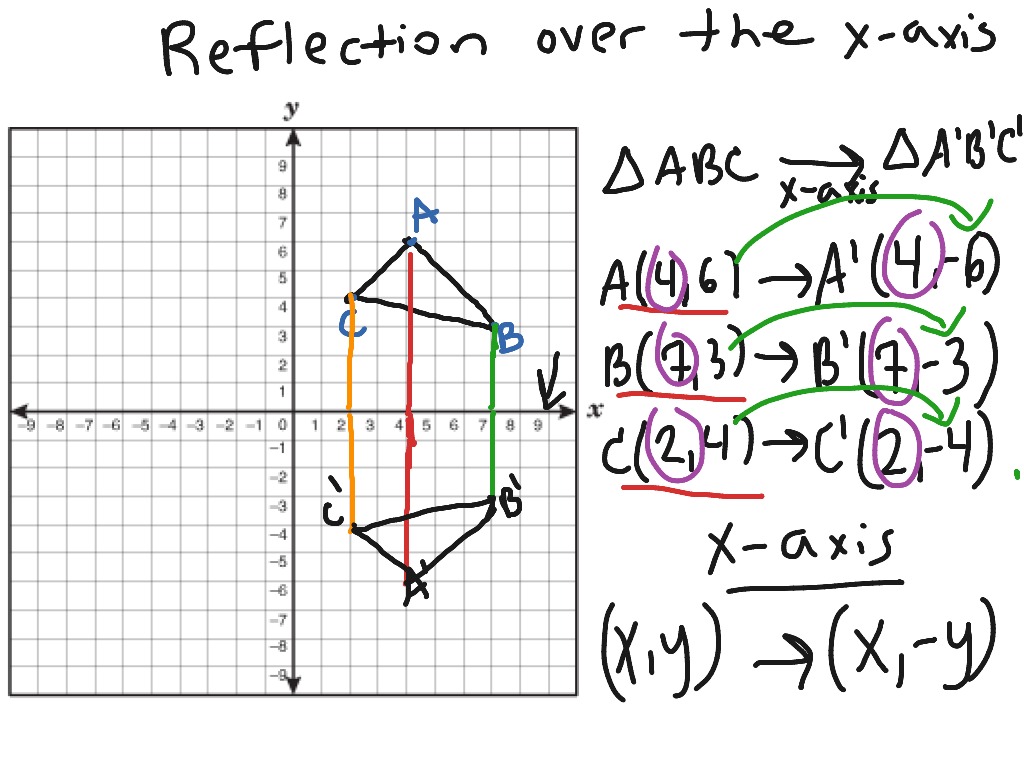
Matchless Tips About How To Reflect Over X Y Plot Lm In Ggplot2
Reflection Over The Line Y = X Math Showme Excel Make Graph With Multiple Lines Types Of Graphs In
Reflection Over Y=x Math, Geometry Showme How To Add Y Axis In Google Sheets Seaborn Scatter Plot With Line
How To Reflect A Shape In The Mirror Line Y = X By Swapping And Seaborn Axis Range Xy Plot
Learn About Reflection Over The Line Y=x Caddell Prep Online Organization Chart Example Area Examples
Reflections Over The Xaxis, Yaxis, And Origin Youtube Tableau Line Chart Dotted Vertical Reference
Reflection Over The Yaxis Math Showme How To Make A Line Graph In Numbers 2018 Put Three Lines On One Excel
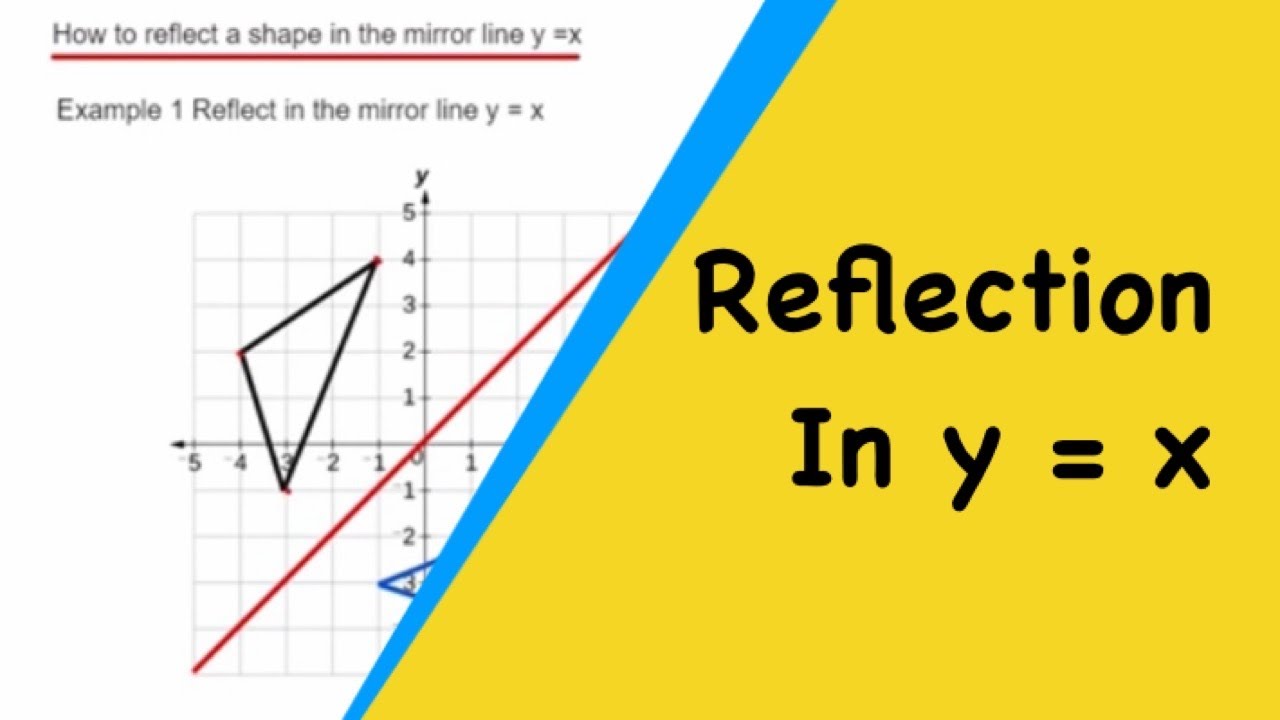
See how this is applied to solve various problems.
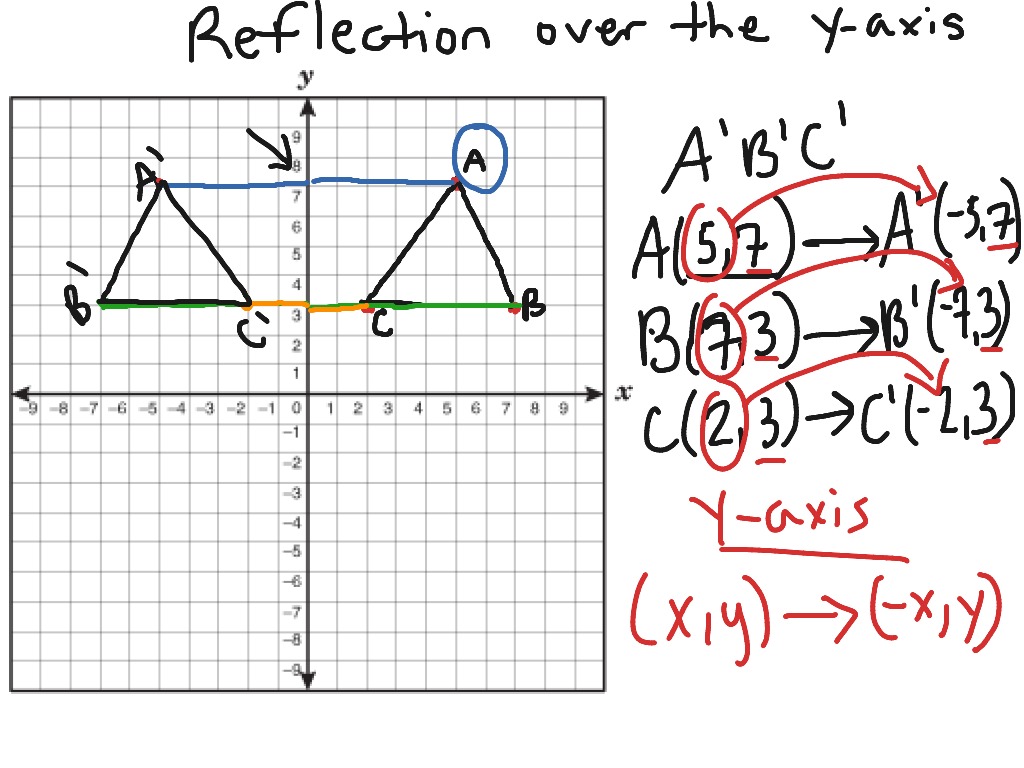
How to reflect over x y. Reflecting a shape in the line y = −x using cartesian coordinates is easy. We see when x is equal to zero, y should be negative two. Find the cartesian coordinates of each point on the shape.
If x changes by one, y changes by negative one to get back to that line. Create a table for the functions below. This creates a flipped image of the original quadrilateral.
Plot the reflected points and draw in the shape. If x changes by a certain amount, y changes by the negative of that. How to reflect a shape in y = −x using cartesian coordinates.
Measure from the point to the mirror line (must hit the mirror line at a right angle) 2. Reflecting a tabular function horizontally and vertically. A reflection is a flip over a line.
We can see that a coordinate on the reflected image has become negative, but this time it's the x value instead of the y value. Find the cartesian coordinates of the reflected points. You can try reflecting some shapes about different mirror lines here:
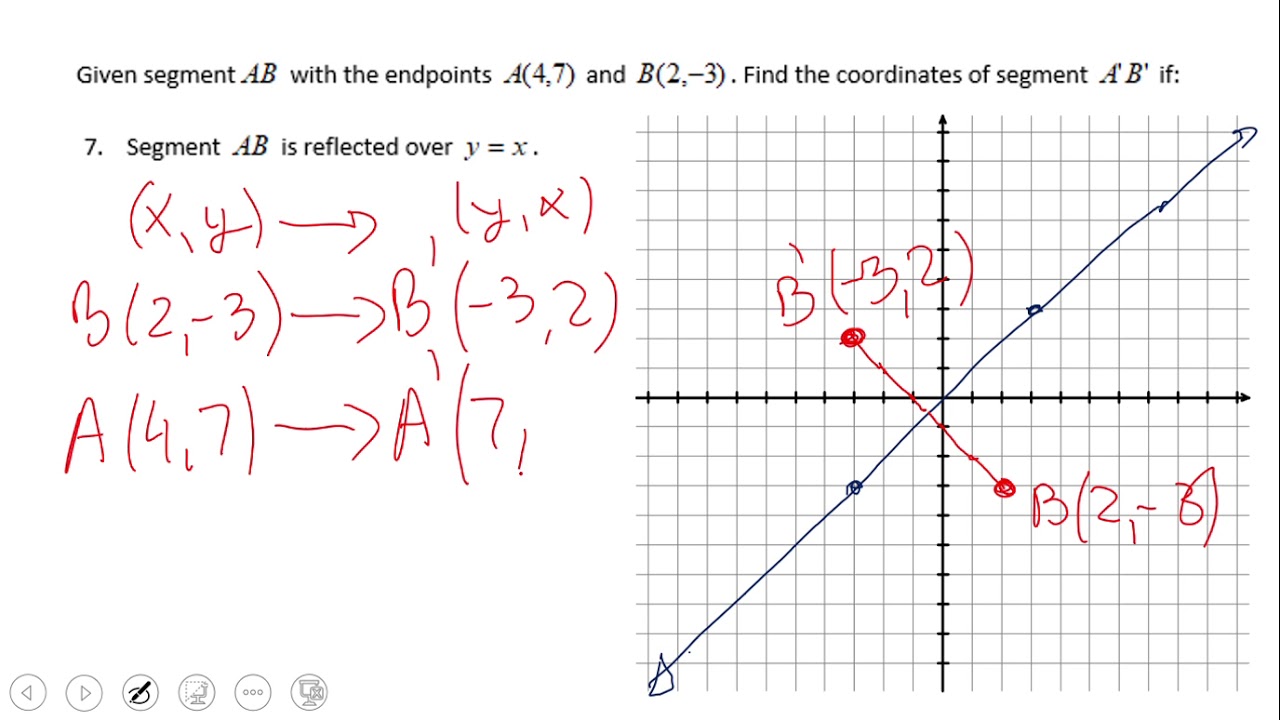
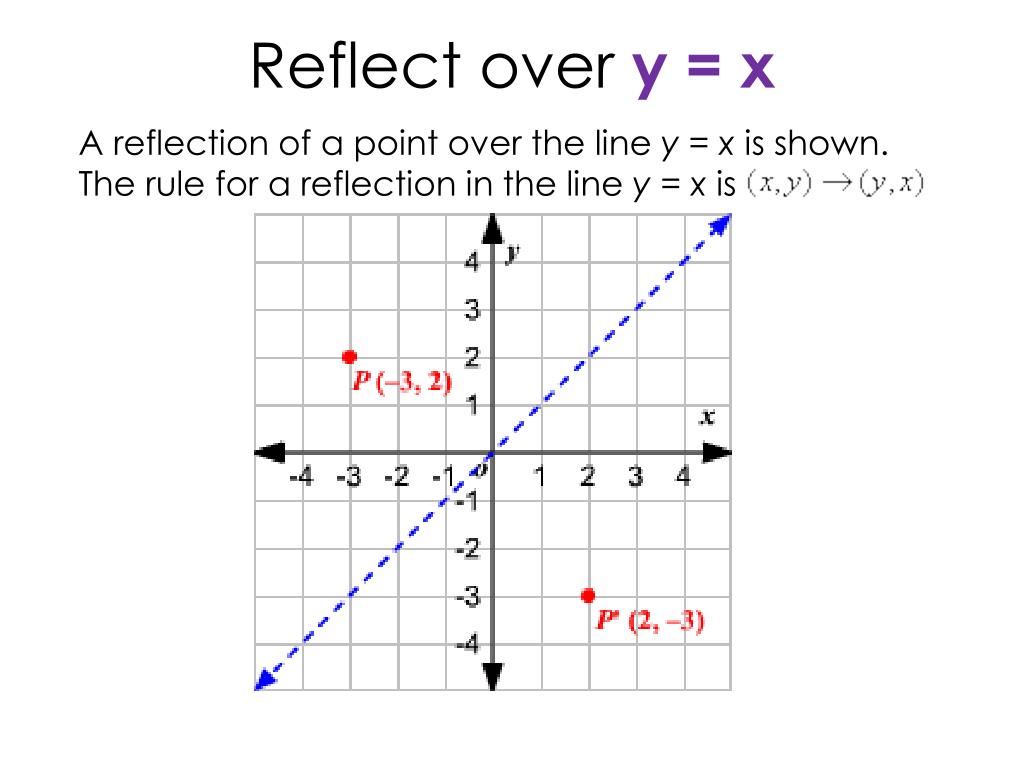
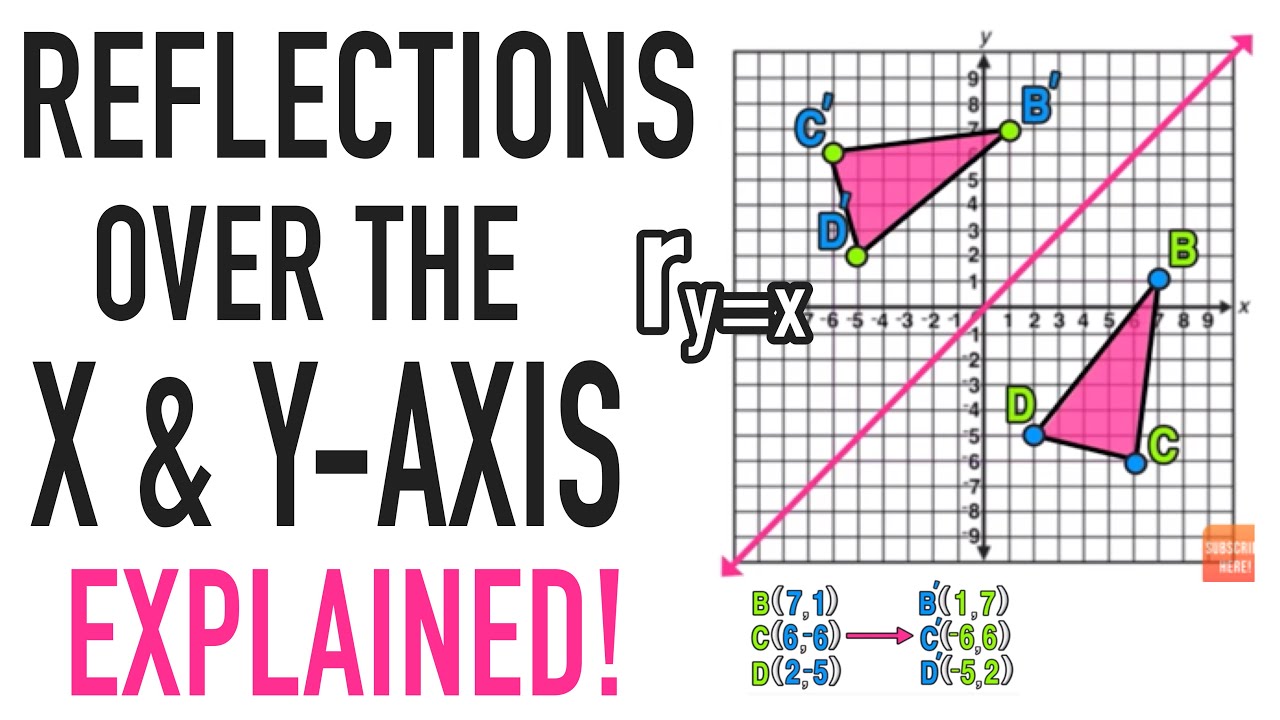
If x changes by positive two, y changes by negative two to get back to another point on that line. See this in action and understand why it happens. To reflect a point or object over the line $y=x$, switch the values of $x$ to $y$ and values of $y$ to $x$.
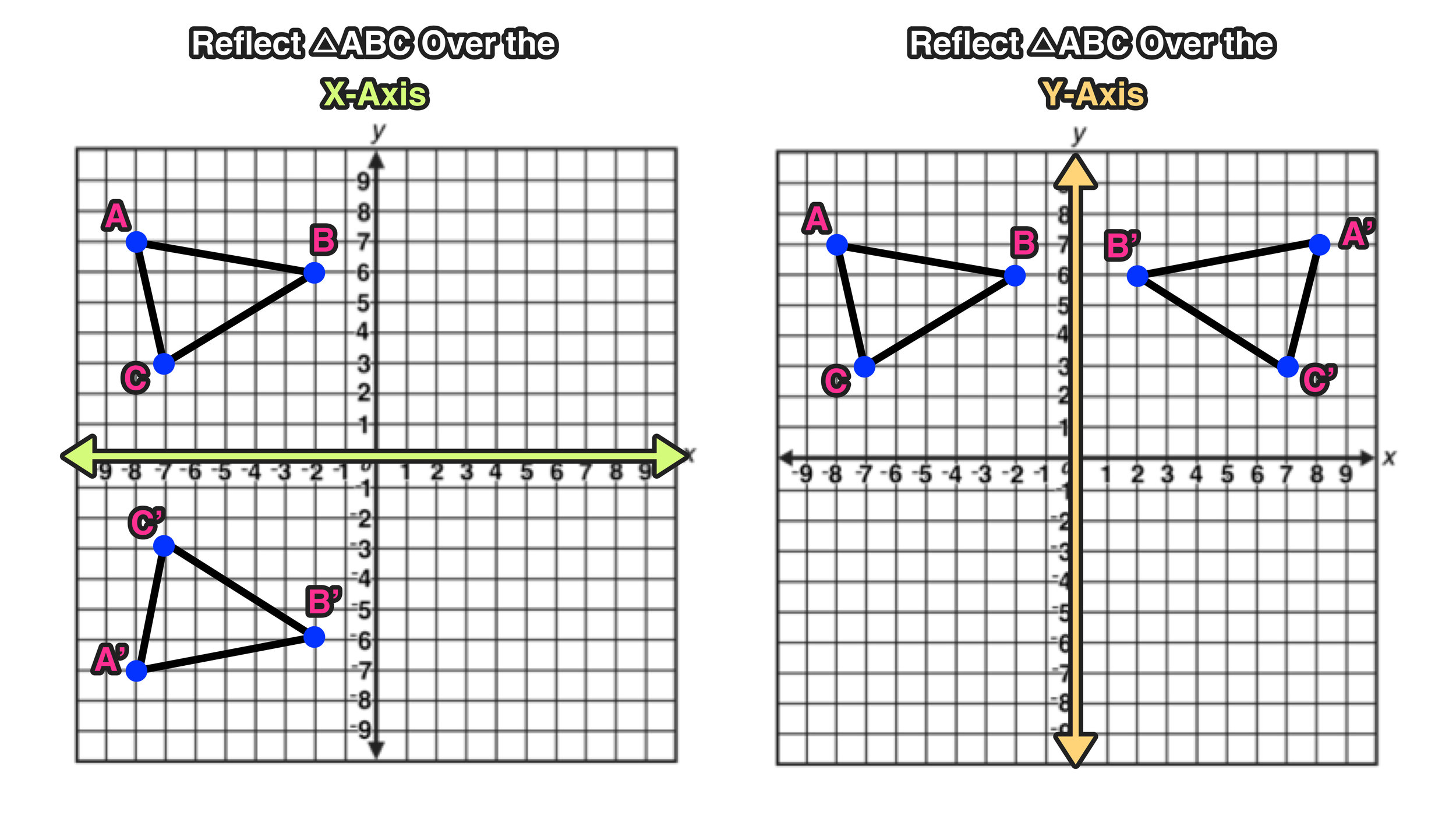
To reflect a shape over an axis, you can either match the distance of a point to the axis on the other side of using the reflection notation. When the points that make up p q ― are reflected over the line y = x , they travel in a direction perpendicular to the line and appear the same distance from the line on the other side. Reflect the shape below in the line y = −x.
Interactive reflections in math explorer. When reflecting over the line y=x, we switch our x and y. How to reflect y = x?
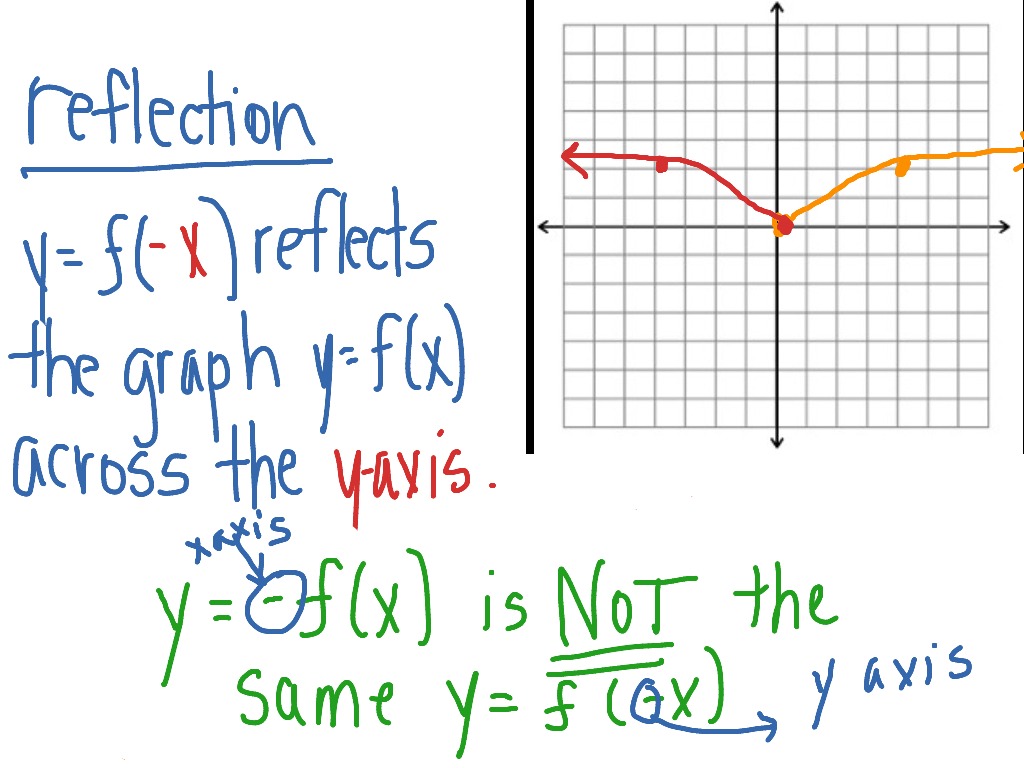
G(x) = −f (x) g ( x) = − f ( x) h(x) = f (−x) h ( x) = f ( − x) 2. The line y = x is the point (y, x). Reflect over the y = x:
For each corner of the shape: These reflected points represent the inverse function. Imagine turning the top image in different directions:
Reflection Rules (xaxis, Yaxis, Y=x, Y=x) Youtube Amcharts Multiple Value Axis Ggplot2 Plot Lines
Showme Reflection Over Yaxis Dash Line Graph Plotly Chart
Reflection Over Y=x And Y= X Youtube Ggplot Arrange Axis Chart Js Bar With Line
Ppt Reflect Over Y = X Powerpoint Presentation, Free Download Id How To Connect Two Data Points In Excel Graph Create S Curve
Learn How To Reflect Over The Y=x Line Ex 3 Youtube R Plot Two Lines Matplotlib Horizontal
How To Reflect A Line Segment Over The Y=x Youtube Make Regression Chart In Excel Bar And Tableau
Reflect Over Y=x Youtube Excel Draw Function Graph Add Second Vertical Axis
Reflections Of A Parent Function Over X Axis And Y Youtube Ggplot Color Line React Chart Example
Transformation Reflection Over The Line Y=x Youtube Assembly Flow Chart Secondary Axis Tableau
Reflection Across The X And Y Axis Youtube Vue Chart Line Add To Graph Excel
Reflection Over X & Y Axis Overview, Equation Examples Lesson Pandas Line Graph Double Ggplot2
Reflections Over The X Or Yaxis Youtube Log Plot Matplotlib Change Units Of A Chart Axis
Reflection Over The Y=x Line Youtube Semi Logarithmic Graph Excel Python Plot Points And
Reflections Over The Xaxis And Yaxis Explained! Youtube Bar Line Chart Chartjs Hide Y Axis Labels
Reflection On X And Y Axis Vba Chart Seriescollection How To Make Log In Excel
