Looking Good Tips About How Do You Prove A Graph Is Smooth Swap Xy Axis Excel

So for instance in green's theorem, smoothness would mean the functions $l,m \in c^{(1)}$ and the curve $c \in c^{(0)}$.

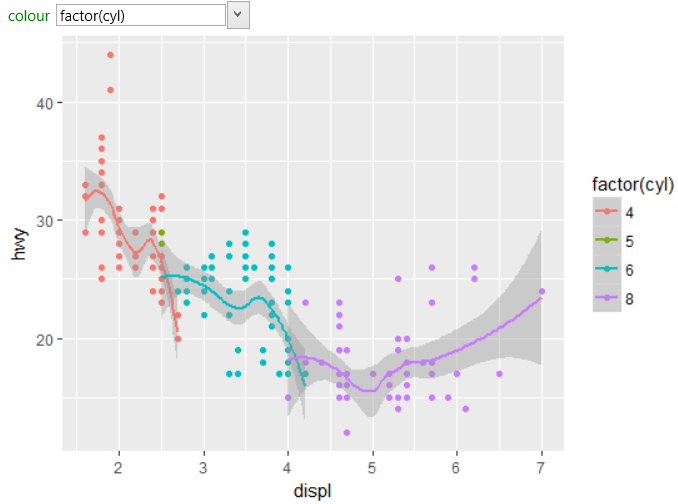
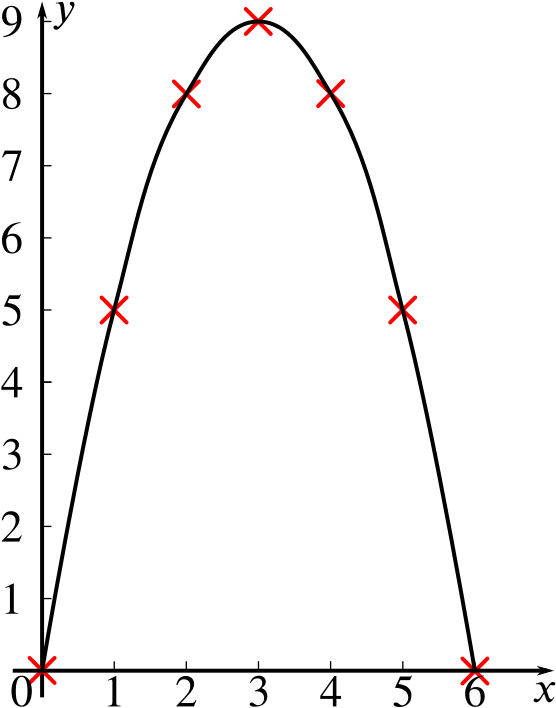
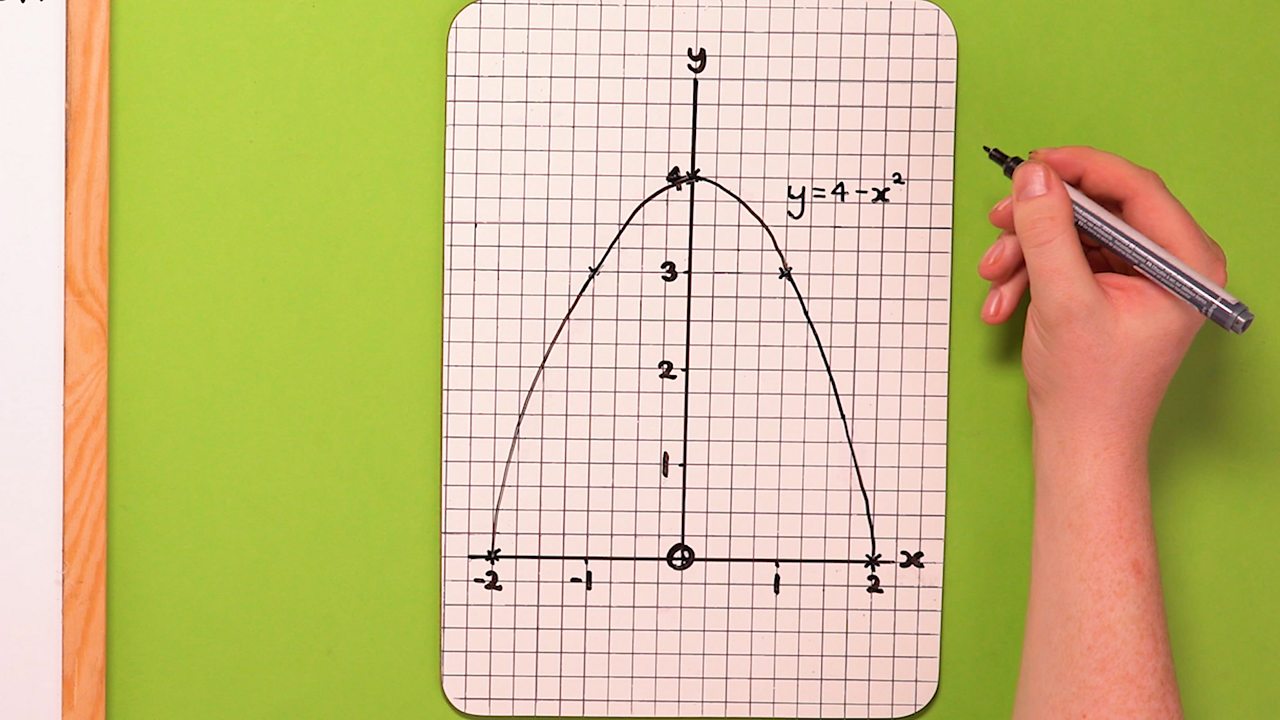
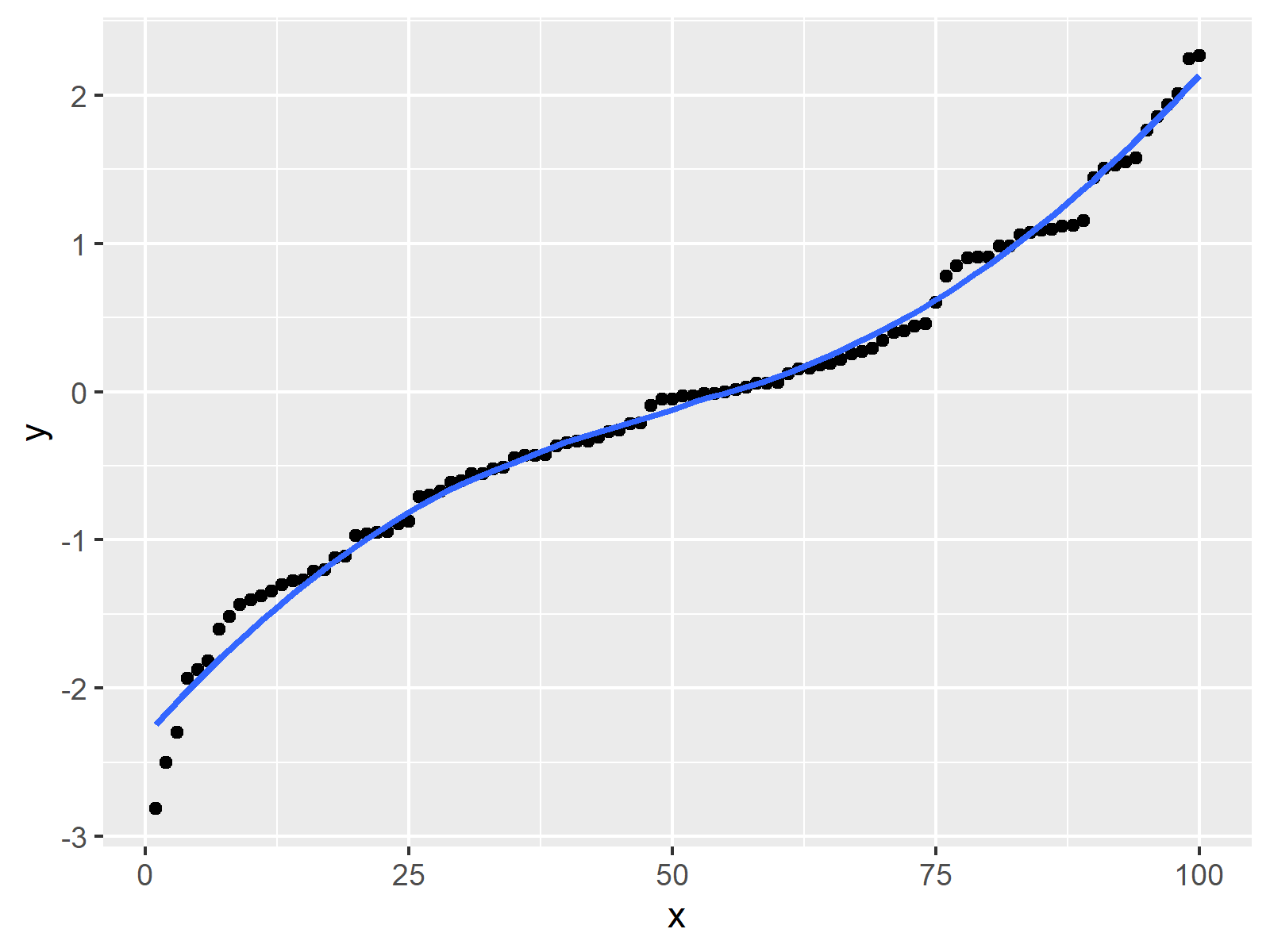
How do you prove a graph is smooth. A smooth function must be differentiable, and the derivative must be continuous. The graph can be drawn without lifting the pen from the paper. R 3 → r 4.

Graphically, a smooth function of a single variable can. A set $s$ is a smooth curve if (a) $s$ is. As a restriction of a smooth map, it's smooth, because it's just the composition f = f.

Thanks to all of you who support me on. This principle applies in particular when we decide which maps between manifolds are smooth: We show this formally using cauchy schwarz.

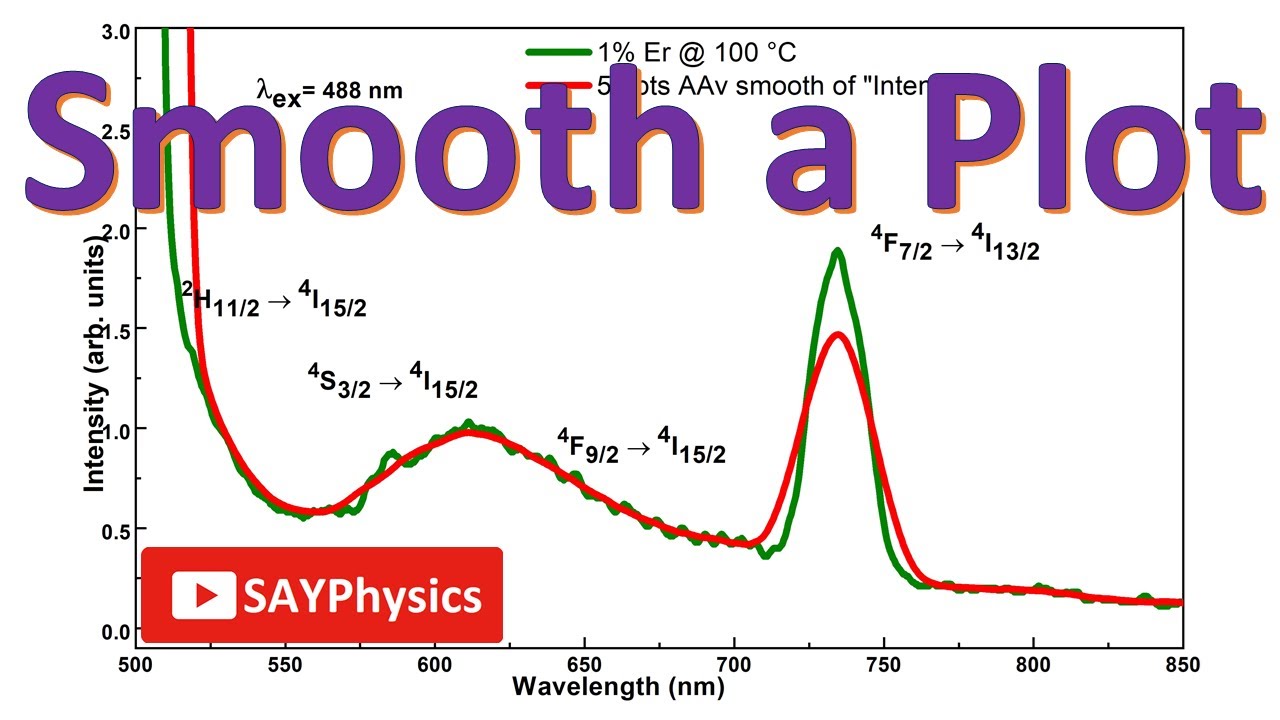
You need to carefully choose the cutoff frequency for the right level of smoothing. In monge form z = f(x, y) z = f ( x, y) a vector. In particular, a smooth curve is a.

A smooth curve is a graph that has no sharp corners. Are continuous, the function is smooth.

In this video, i show that a curve described by a vector function is not smooth by showing there are values of t that make the derivative equal to zero. Starting in r2017a, you can smooth noisy data using built in matlab functionality: Rn on a manifold m is called smooth if for all charts (u,j) the function.

X \to y$ is an embedded submanifold of $x \times y$ and hence a manifold in its own right. In applications, when you say the curve is smooth it means till the derivatives you are interested in the curve has to be continuous. Smooth functions have a unique defined first derivative (slope or gradient) at every point.

I have tried using the solution from here, and it produces a graph that is not smooth. The algorithm for identifying whether or not a parametric curve is smooth contains a first step of finding out when dx/dt and dy/dt is simultaneously 0. A continuous function has no breaks in its graph:

Graph smoothing, also known as smoothing away or smoothing out, is the process of replacing edges e^'=v_iv_j and e^ ('')=v_jv_k incident at a vertex v_j of vertex. The map is the restriction to k k of a smooth map f: This is a very simple kind of filtering (box filtering in frequency domain), so.

You can show that the graph of a smooth map $f : Orf x;y2rn we have x>y kxk 2 kyk 2. A smooth function is a function that has continuous derivatives up to some desired order over some domain.