Outstanding Tips About What Is A Parabola Vs Hyperbola Excel Chart Add Gridlines

In the case of a parabola, the line passing through the focus and perpendicular to the directrix is known as an axis of symmetry.

What is a parabola vs hyperbola. Looking at the left hand branch in this diagram: In the polar form r = ℓ 1+e cos θ r = ℓ 1 + e cos. A parabola is a curve formed when a plane cuts a cone parallel to the cone side.

A hyperbola is created when a plane cuts a conical surface parallel to the axis. When we tilt the plane so that its angle matches the slope of the cone, we get a parabola. A hyperbola’s center is the midpoint of the major axis.

Parabola is the locus of all points which are equally spaced from a fixed line (called directrix) and a fixed point (called the focus). While they share some similarities, they have distinct differences. A hyperbola, a type of smooth curve lying in a plane, has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows.

The most obvious difference between their graphs is that a hyperbola has two curves that mirror each other and open in opposing directions. The important feature of a hyperbola lies in the relationship between the distance from any point on the curve to two fixed focal points that are also known as foci, and that difference in distances remains constant for all points on the. The point halfway between the focus and the directrix is called the vertex of the parabola.

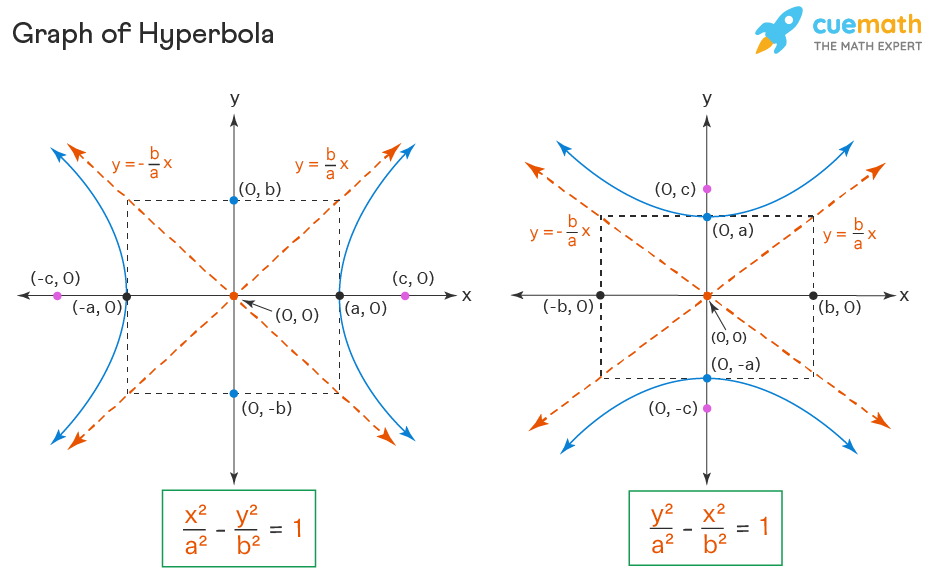
Similarly, the conic section called hyperbola is formed when a plane divides the cone parallel to its axis. In order to understand why, let's have an equation of a hyperbola and an ellipse, respectively: The parabola is a single open curve with eccentricity one, whereas a hyperbola has two curves with an eccentricity greater than or equal to one.

X^2/9 + y^2/4 = 1. Difference between parabola and hyperbola. A hyperbola is the set of points in a plane whose distances from two fixed points, called foci, has an absolute difference that is equal to a positive constant.

In a hyperbola, the two arms or curves do not become parallel. A parabola, on the other hand, has only one curve. Pf is the distance p to f.

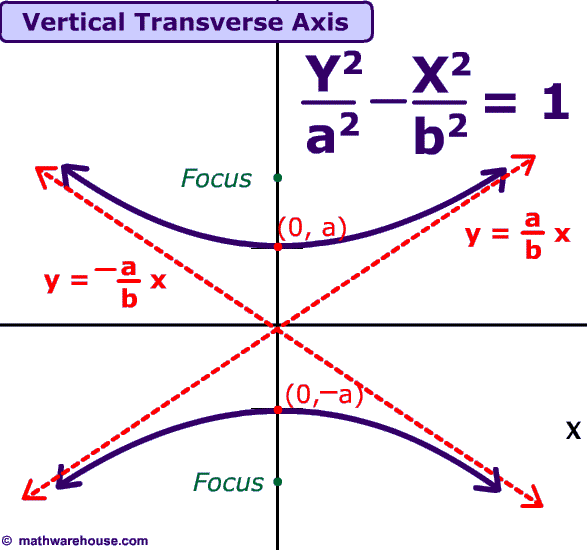
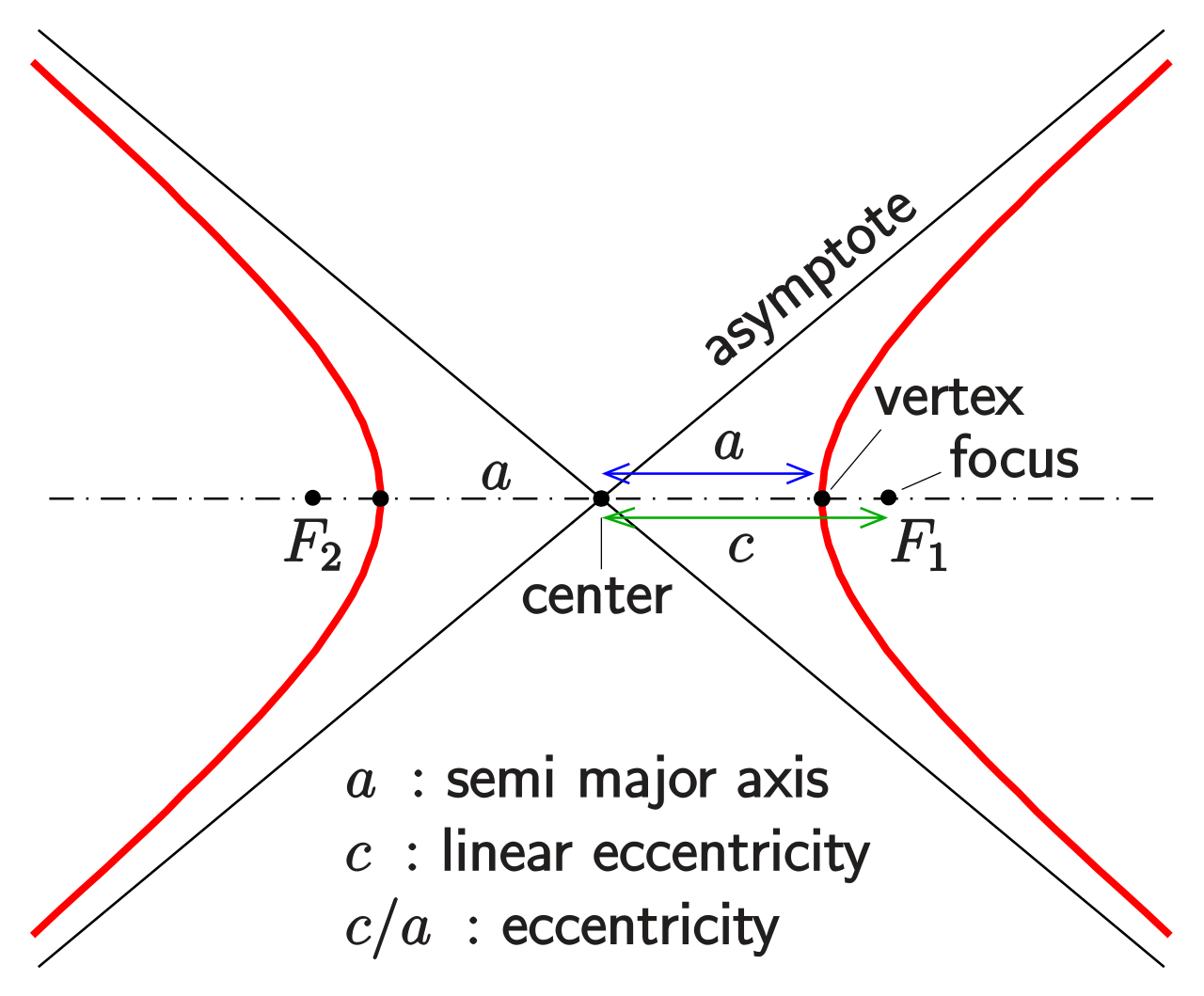
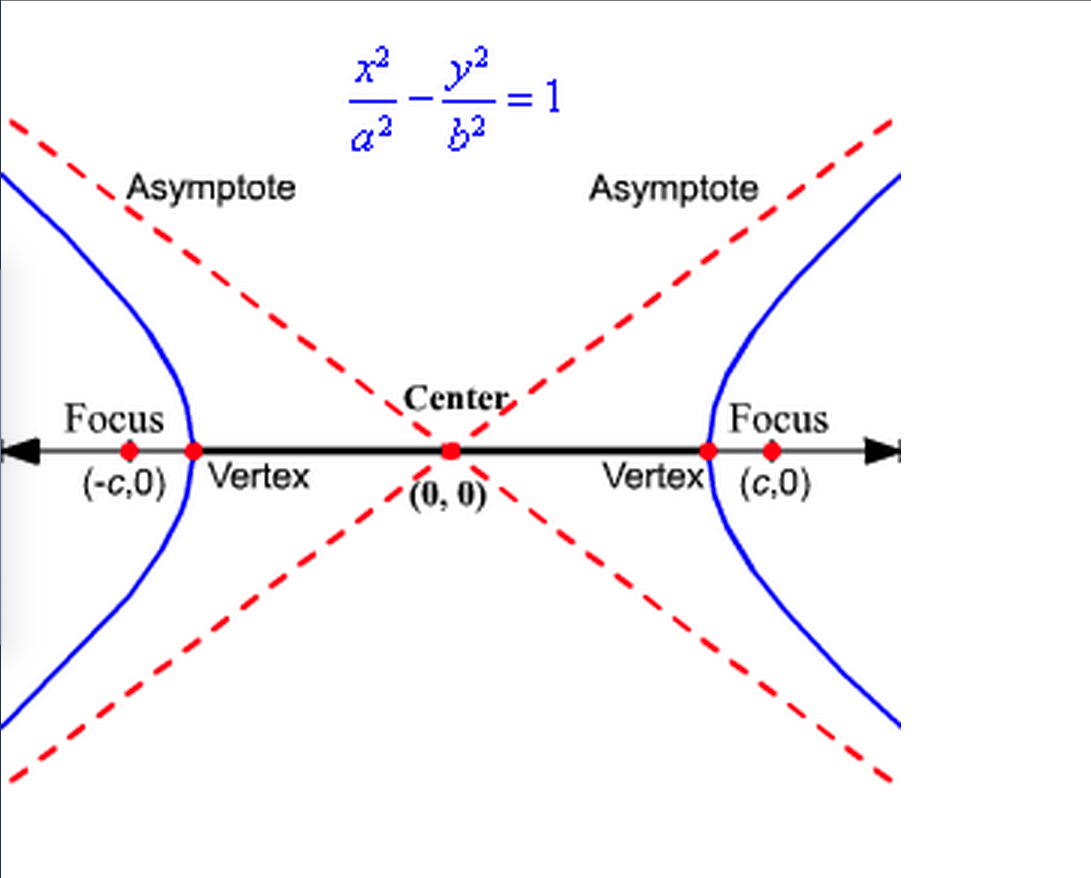
Unlike the parabola, a hyperbola comes into existence when a plane divides a cone parallel to its axis; The standard form of a hyperbola can be used to locate its vertices and foci. Unlike an ellipse, the foci in an hyperbola are further from the hyperbola's center than are its vertices, as displayed below:

Hyperbola and parabola are both conic sections, but they have distinct characteristics that set them apart. |pf − pg| = constant. A hyperbola is a set of points whose difference of distances from two foci is a.

A parabola can be described as a set of points in a plane which are equidistant from a straight line or directrix and focus. A hyperbola is defined as the set of all points in a plane, such that the difference of the distances from two fixed points, called the foci, is constant. The section of the cone called a parabola is formed if a plane (flat surface) divides the conical surface, which presents parallel to the side of the cone.