Out Of This World Tips About How To Tell If A Slope Is Increasing Or Decreasing Combo Graph Excel 2010

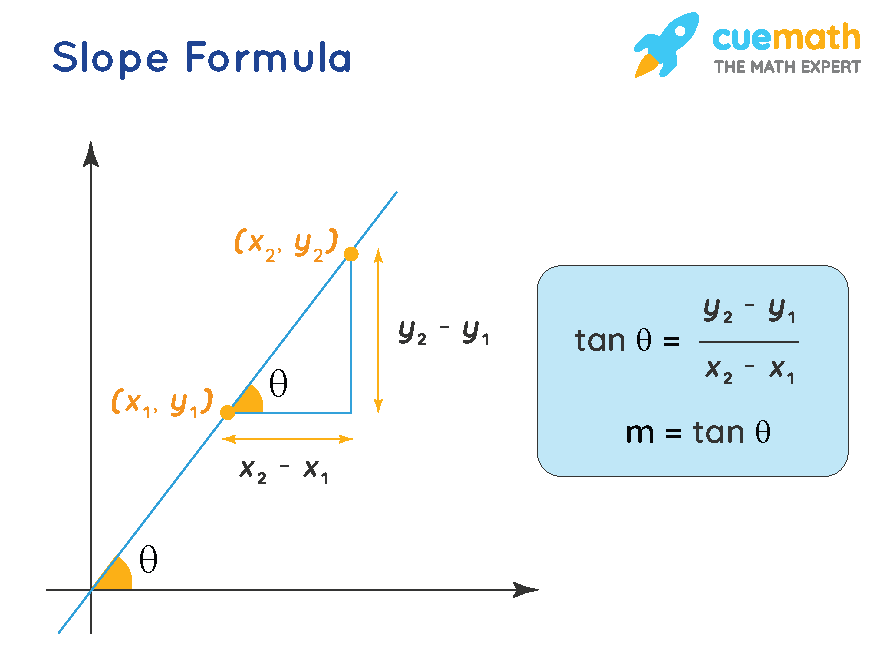
Calculate the slope:

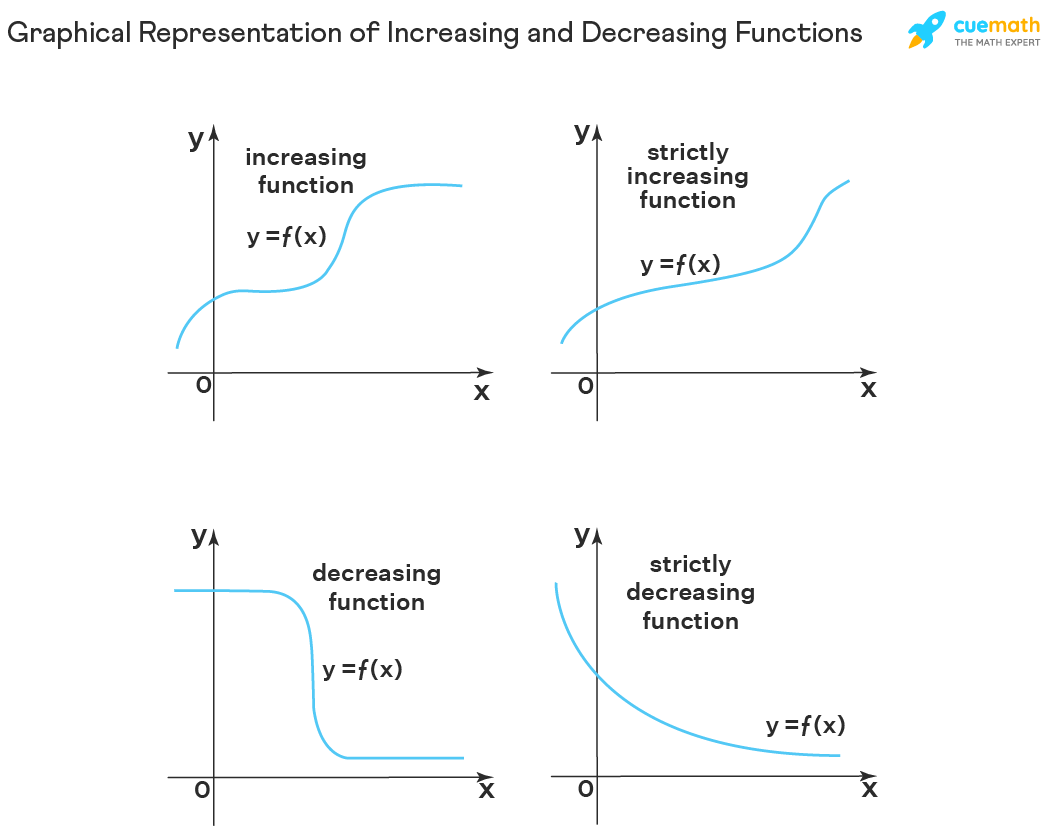
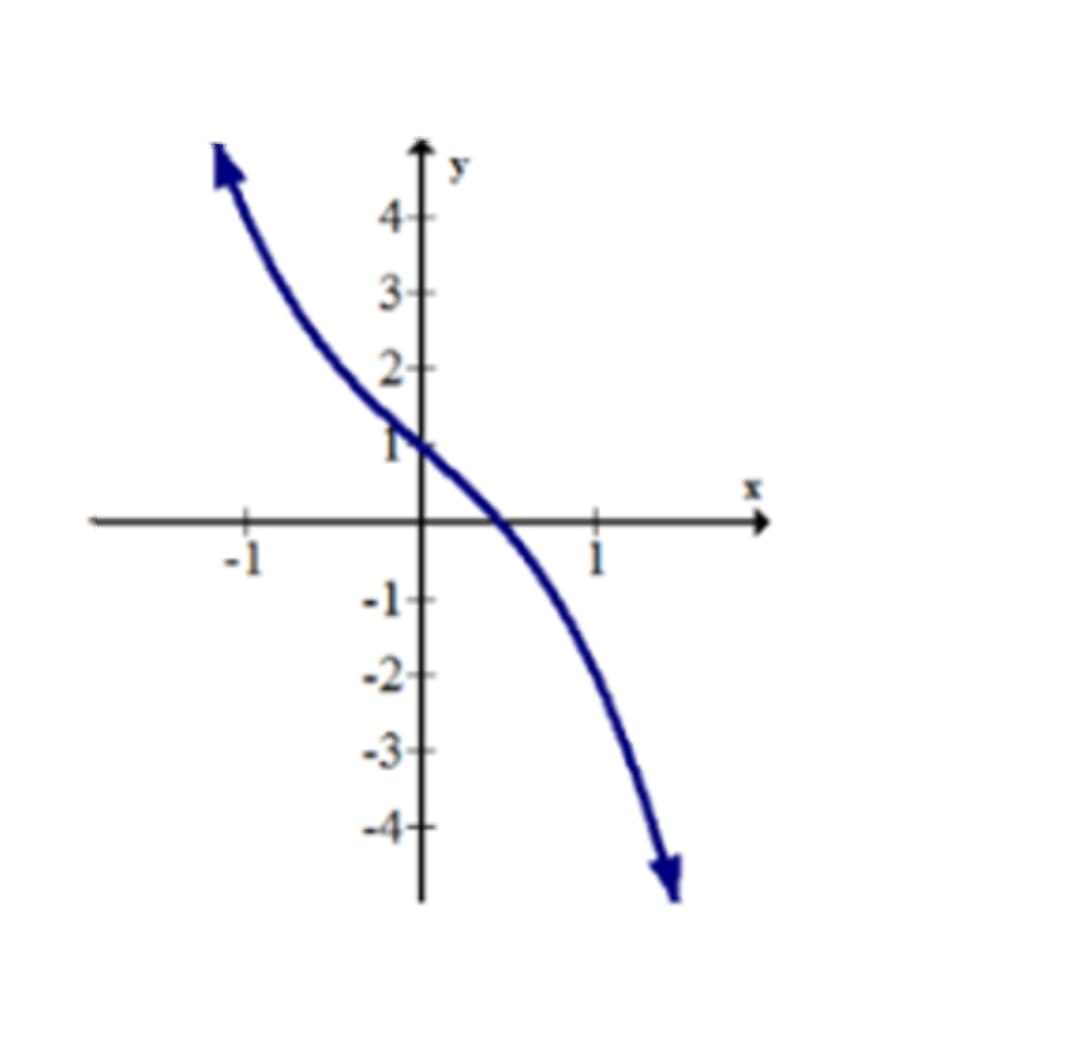
How to tell if a slope is increasing or decreasing. In algebra, the slope can indicate if a function is increasing or decreasing. A graph is decreasing if it goes downwards from left to. How do you know if a graph is increasing or decreasing?

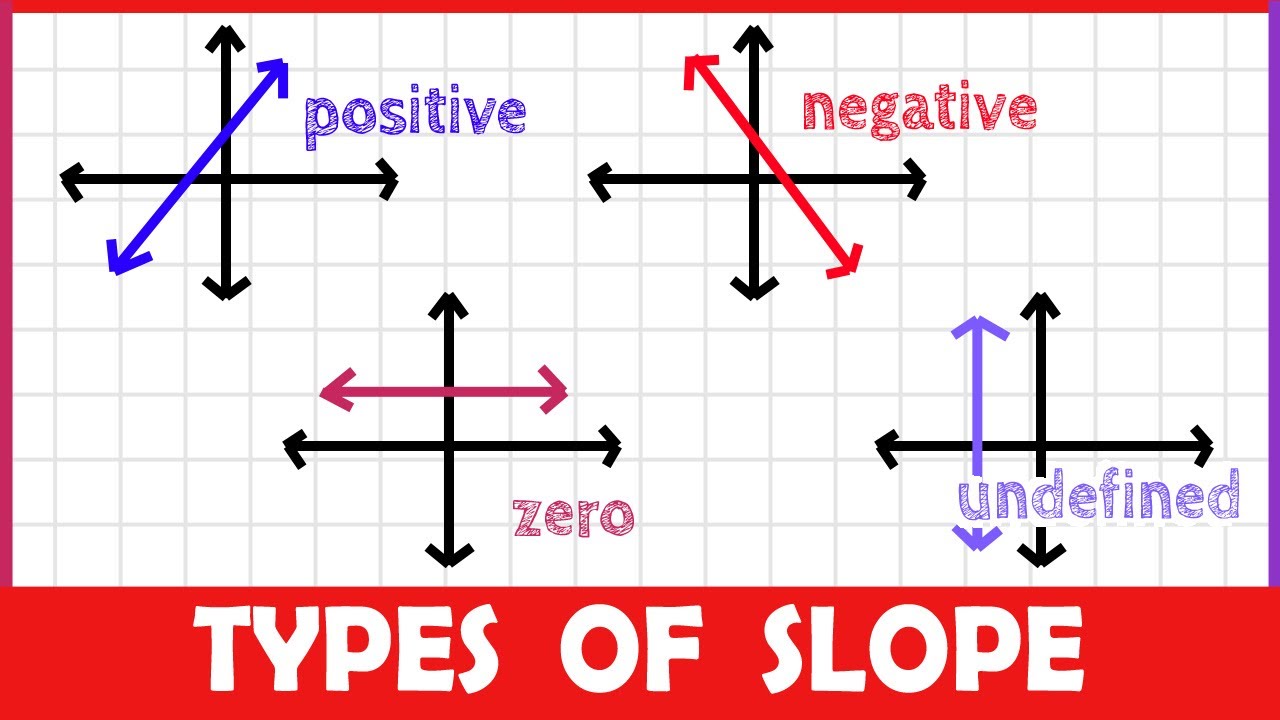
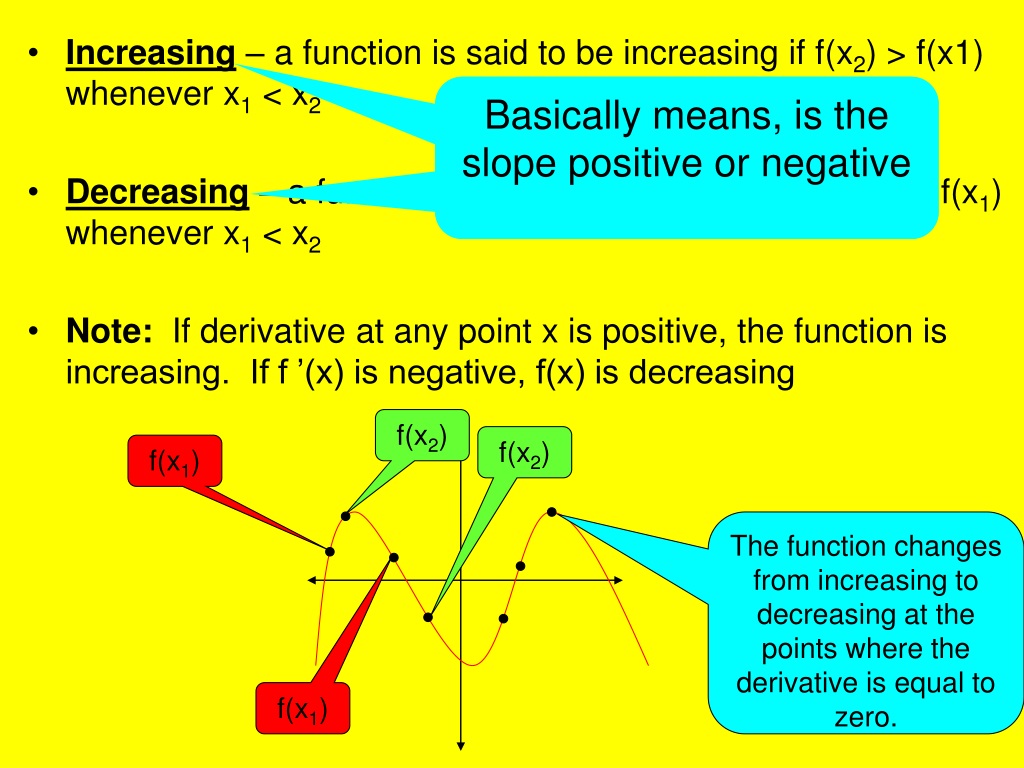
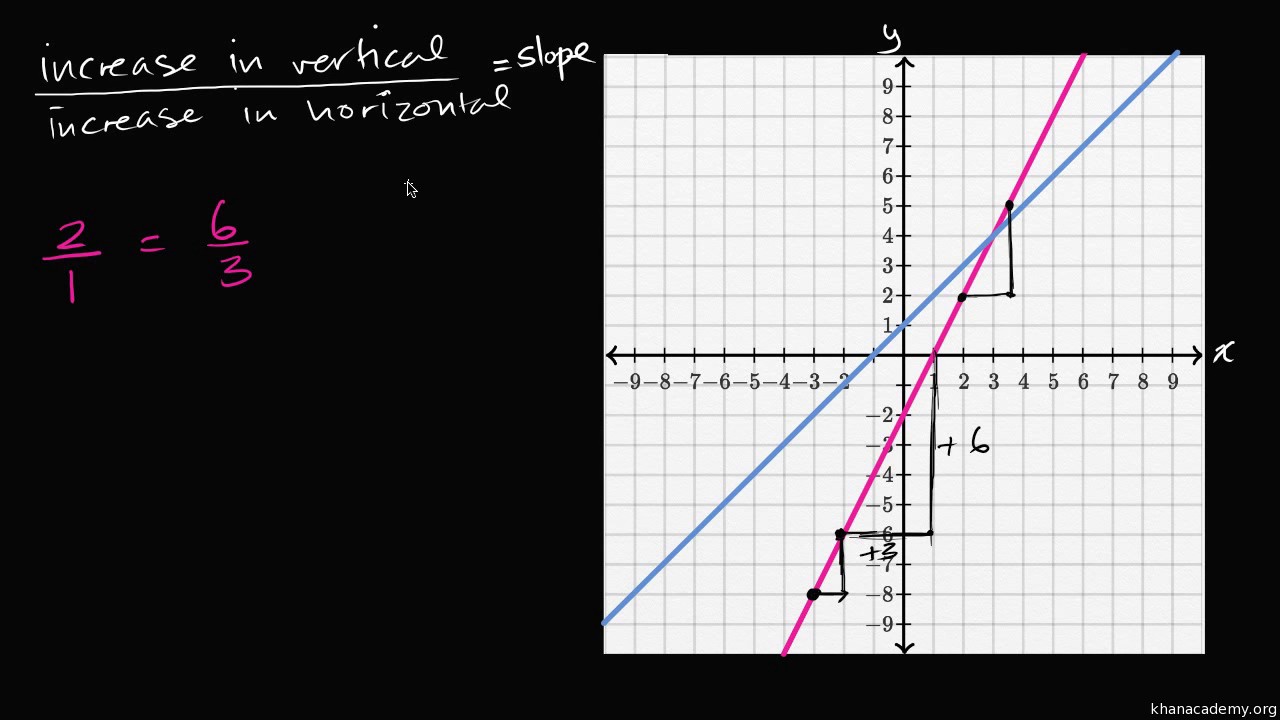
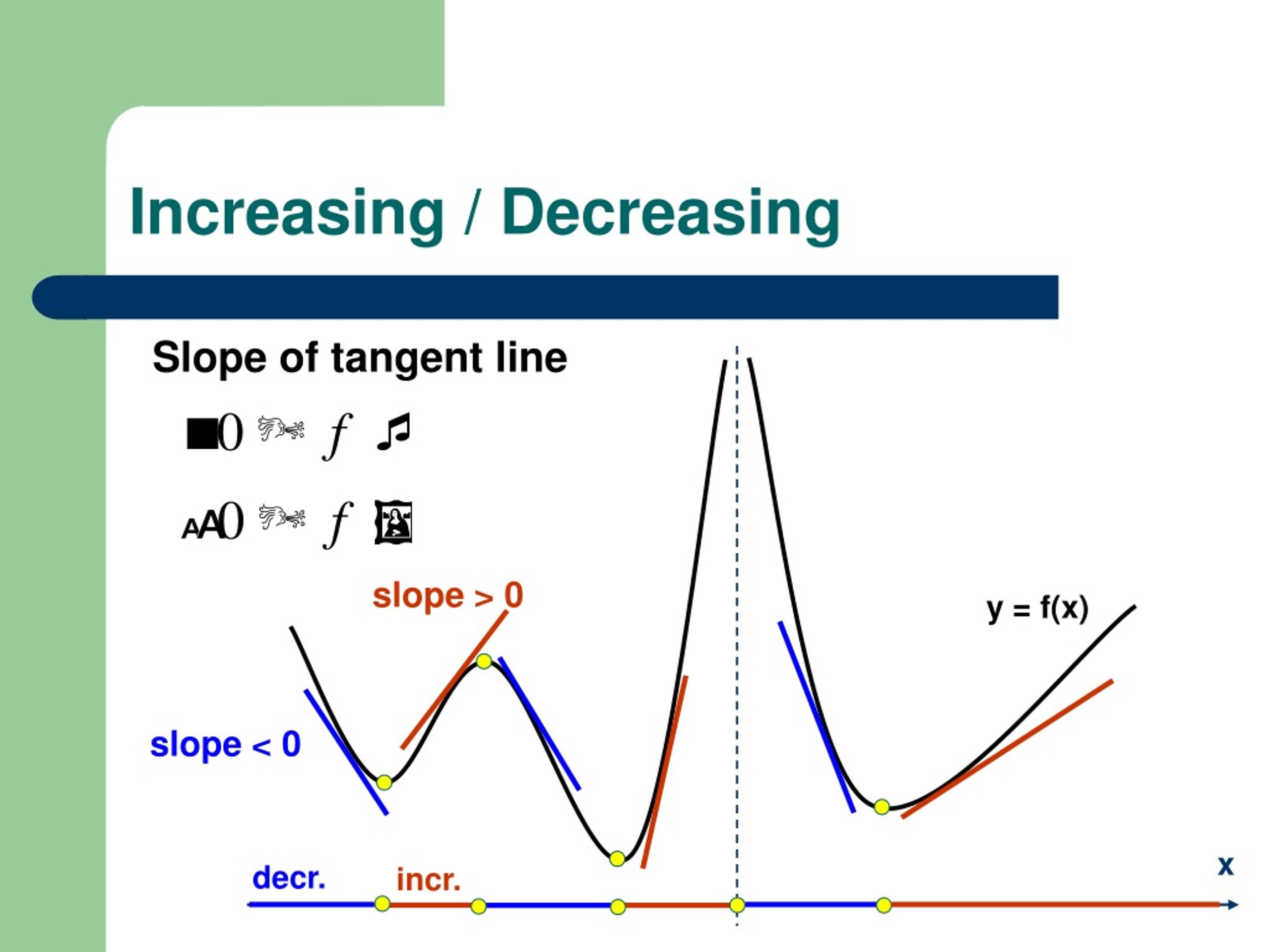
The graph of an increasing function has a positive slope. Use the slope formula to find the slope of a line between two points; Increasing is where the function has a positive slope and decreasing is where the function has a negative slope.

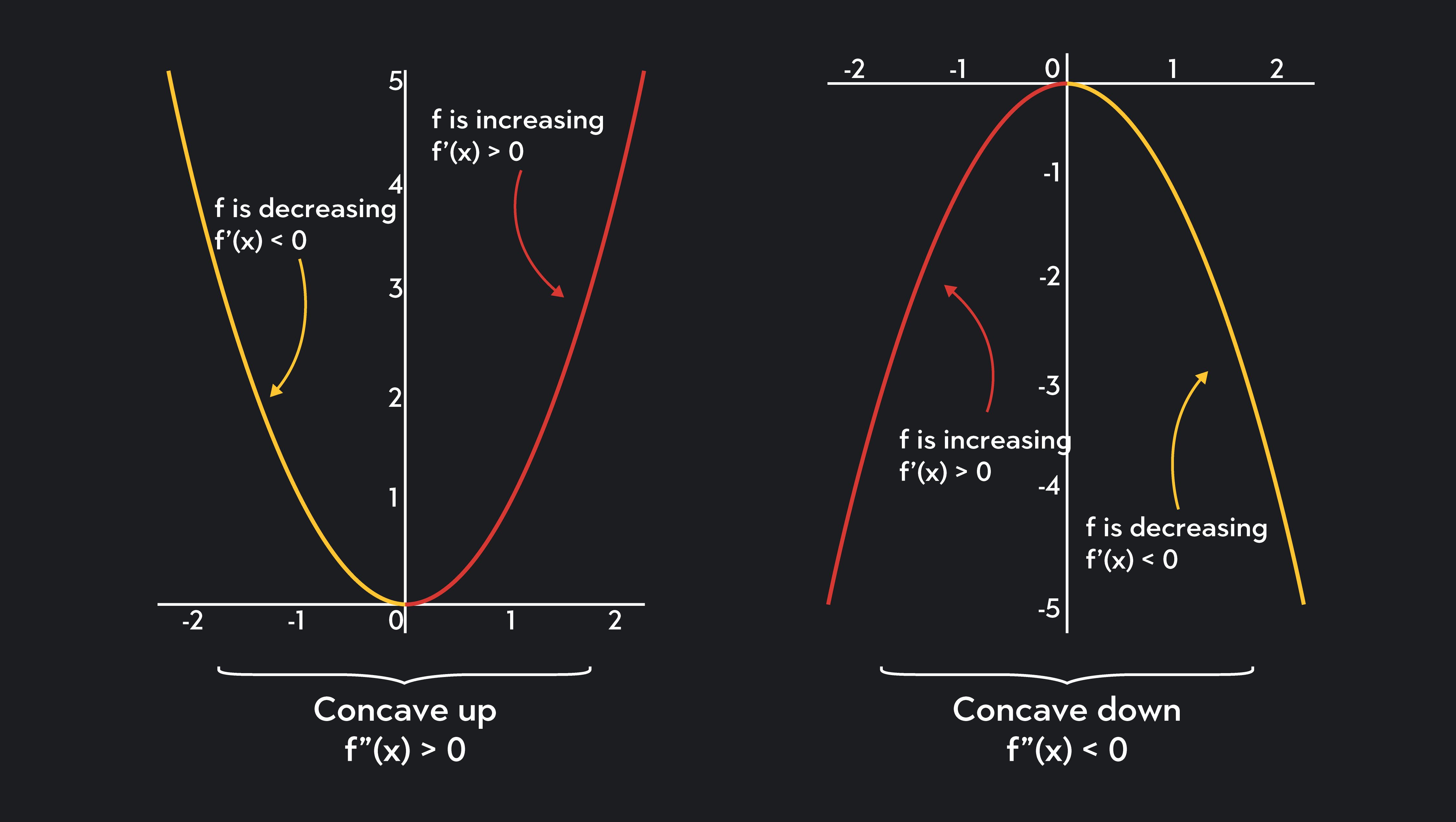
If x1 < x2 ⇒ f (x1) ≤ f (x2) ∀ x1 and x2 ∈ i. The three definitions below explain what happens when you increase all production inputs by a multiplier. Continuing with the idea that the slope of the tangent is the derivative:

Applying the first derivative test, the critical number is 113−−√ 11 3. And how to calculate slope angle of a line in python? That is, when x increases, y decreases, and when x decreases, y increases.

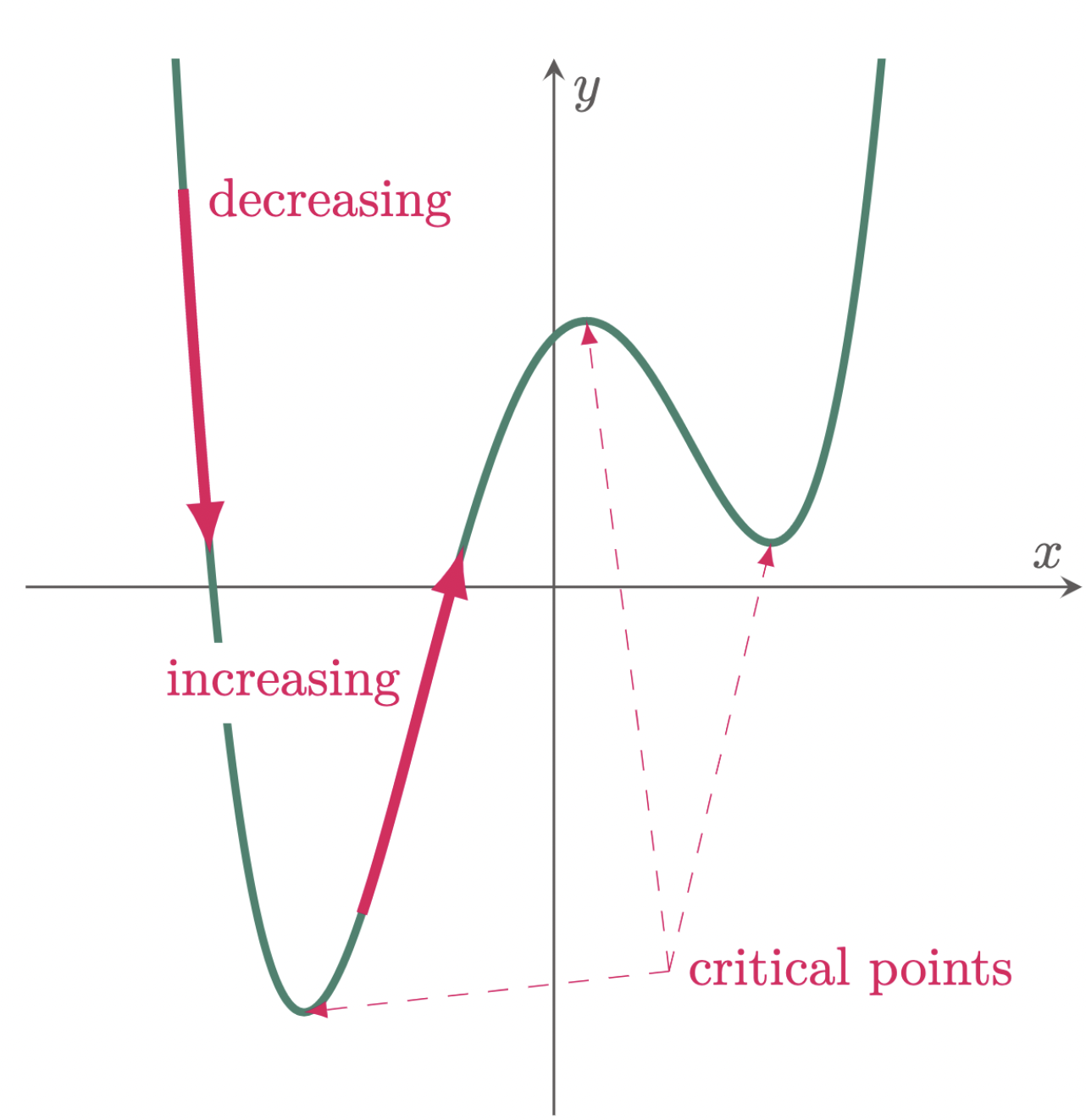
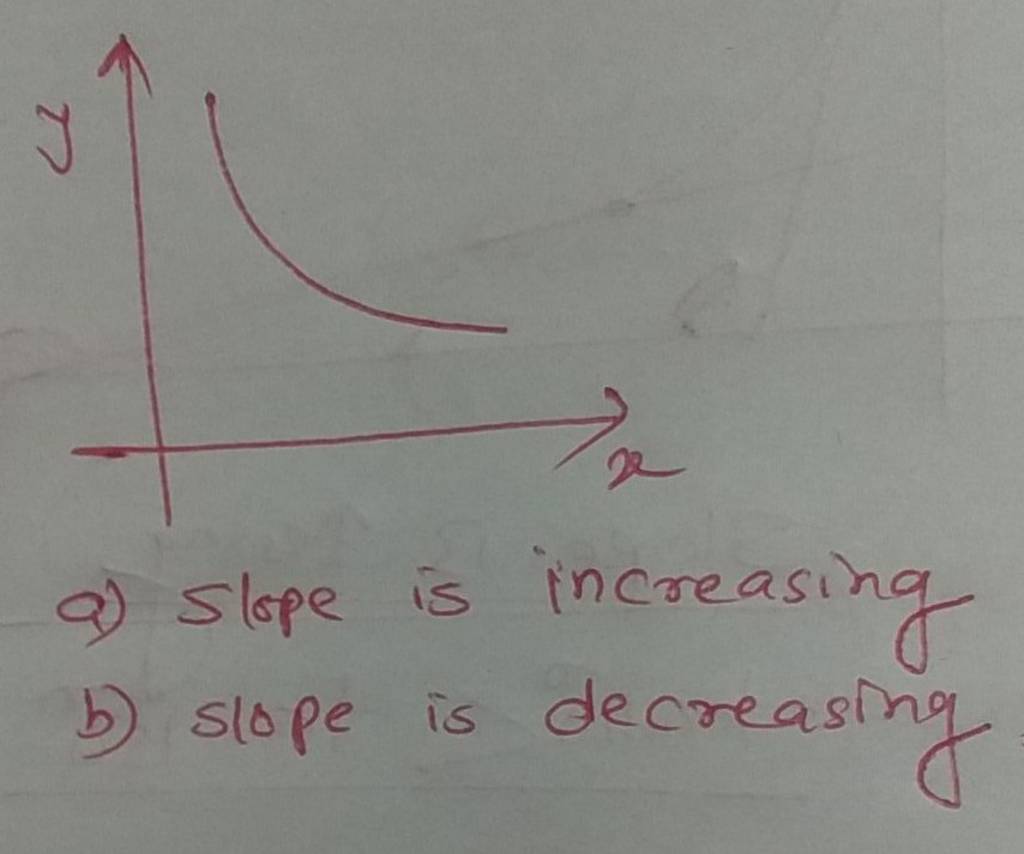
Find intervals on which \(f\) is increasing or decreasing. A negative slope means that two variables are negatively related; For a decreasing function , the slope is negative.

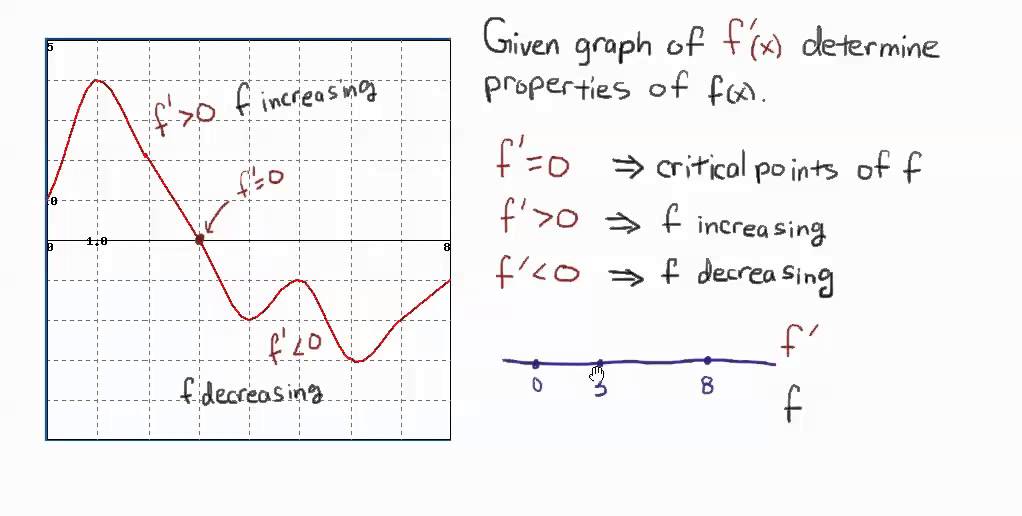
The slope m tells us if the function is increasing, decreasing or constant: Some common examples of increasing functions include linear functions with positive slope (such as y = mx + b), exponential functions (such as y = ax, where a is a positive constant), and power functions (such as y = xn, where n is a positive integer). [latex]f\left(x\right)=mx+b\text{ is an increasing function if }m>0[/latex].

The function appears to be increasing from [latex]t=1[/latex] to [latex]t=3[/latex] and from [latex]t=4[/latex] on. Find the slope of horizontal and vertical lines; Since slope is defined as the rate of change, then getting the maxima of the function's derivative will indicate where it is increasing at the greatest rate.

Is finding a slope for the line is the best way? Using the key idea 3, we first find the critical values of \(f\). The function would be positive, but the function would be decreasing until it hits its vertex or minimum point if the parabola is upward facing.

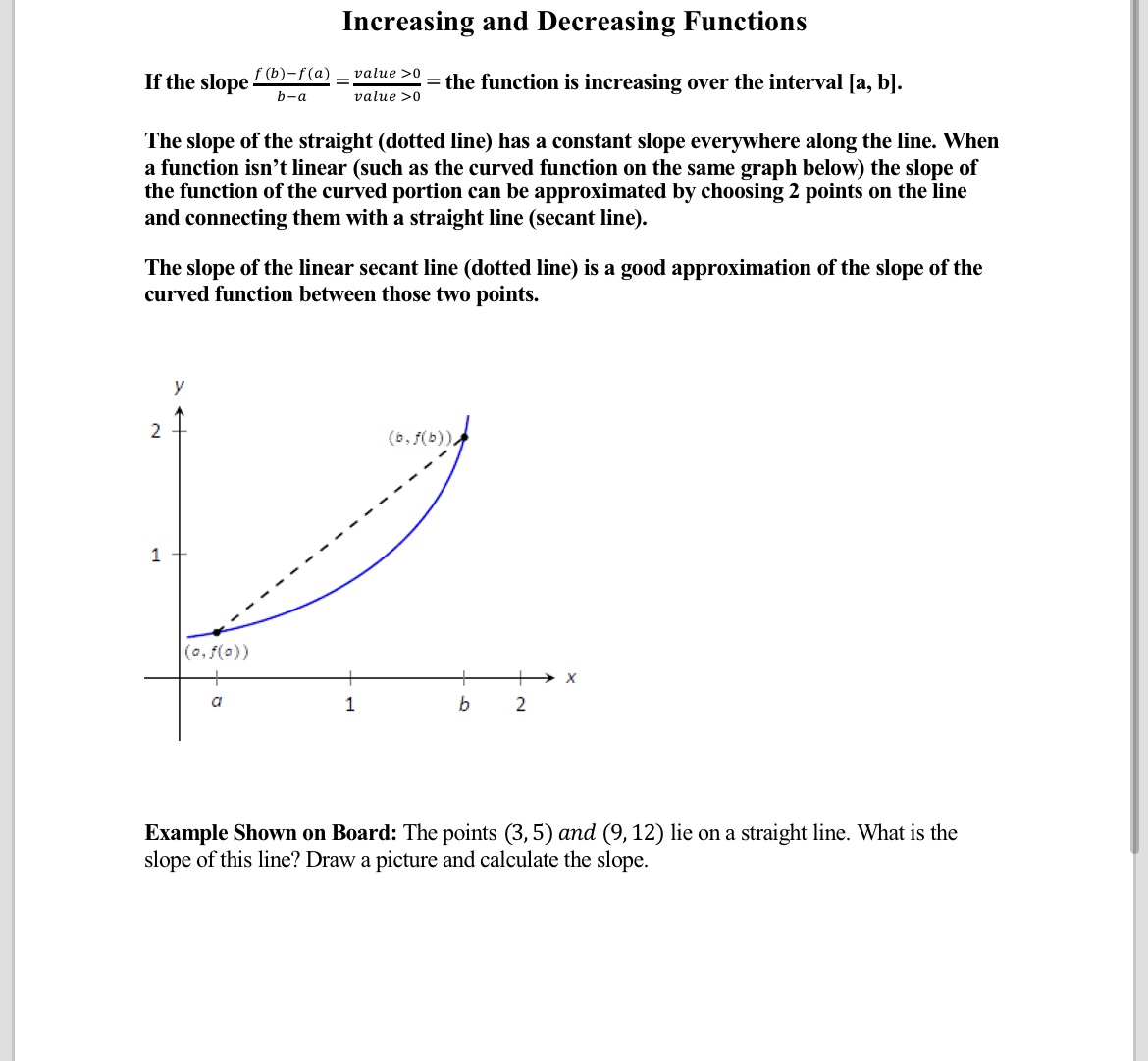
A function is increasing where its derivative is positive, and is decreasing where its derivative is negative. A line with a positive slope slants upward from left to right as in (a). The slope of a linear function, for.

Use \(m = \frac{\text{rise}}{\text{run}}\) to find the slope of a line from its graph; In other words, while the function is. If the function is decreasing, it has a negative rate of growth.