Glory Info About How Do You Know If A Graph Is Smooth Kibana Area Chart

Graphs are continuous and smooth;

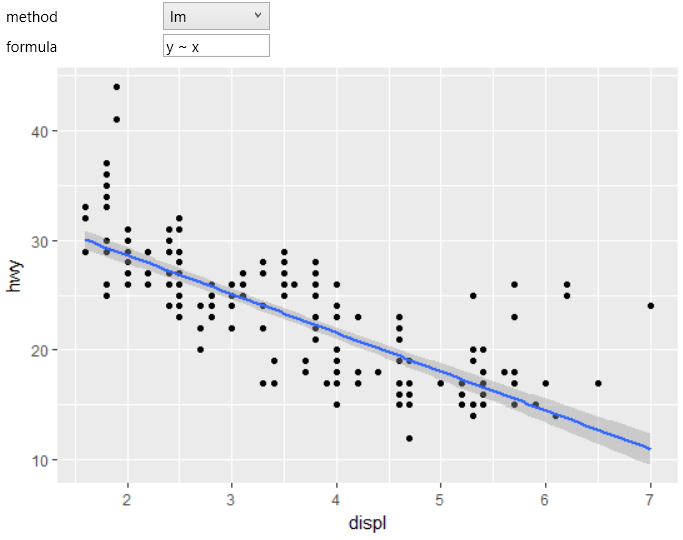
How do you know if a graph is smooth. A curve is said to be smooth if it has no singular points, in other words if it has a (unique) tangent at all points. If it's important to display the exact values, then the straight lines do a much better job. Definition (smooth curve) let $\gamma\colon [a,b] \to \mathbb{r}^2$ a curve (continous function).

There is a cusp at the associated point on the graph of ⇀ r(t), or. In fact, for $x\rightarrow0^{\pm}$, $f(x)\sim \pm x$. This one is not smooth:

My textbook points at that there are functions where dx/dt and dy/dt are both 0 and still smooth. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. It describes a curve’s appearance, rather than any mathematical properties.

It looks like its graph has a sharp corner in $x=0$. It is worse than a corner! You can draw a graph and see, that it.

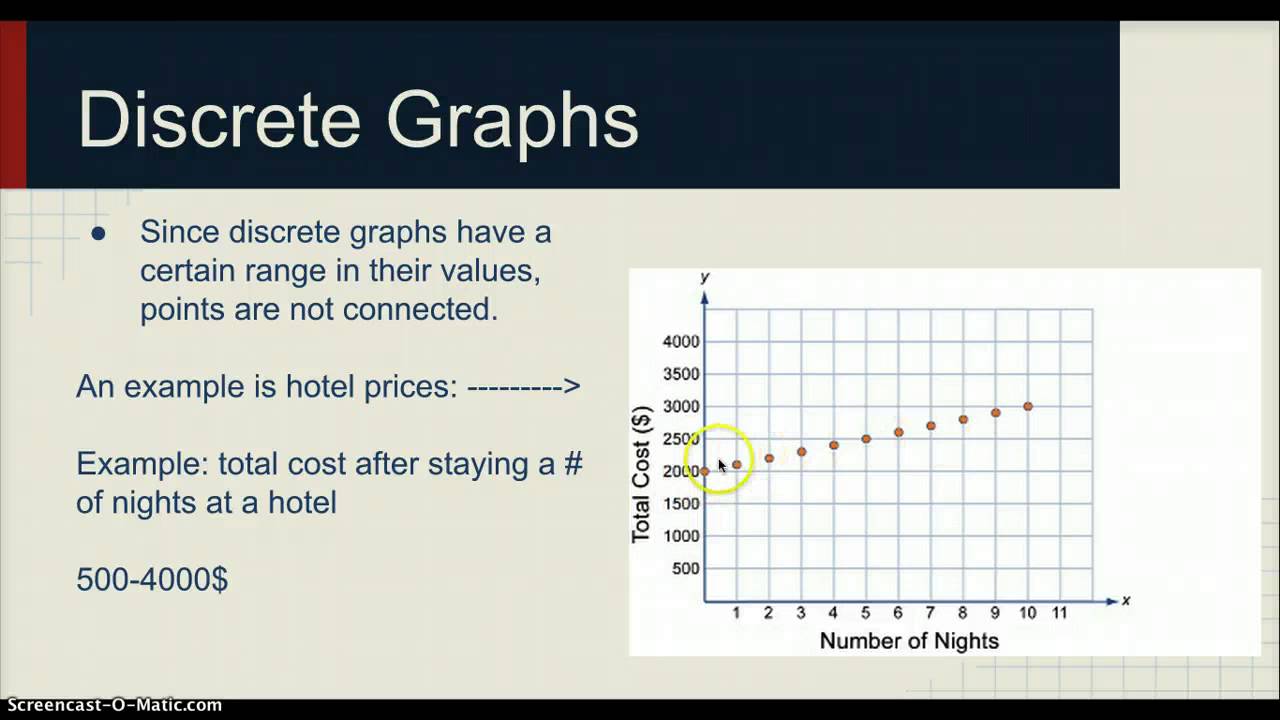
Go through (0,0), (1,1) and (−1,1); What are the other steps? A graph for a function that's smooth without any holes, jumps, or asymptotes is called continuous.

Above (or equal to) 0; So for instance in green's theorem, smoothness would mean the functions $l,m \in c^{(1)}$ and the curve $c \in c^{(0)}$. The formal definition of a smooth curve is:

In applications, when you say the curve is smooth it means till the derivatives you are interested in the curve has to be continuous. A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. The motion reverses itself at the associated point, causing the motion to travel back along the same path in the opposite direction, or.

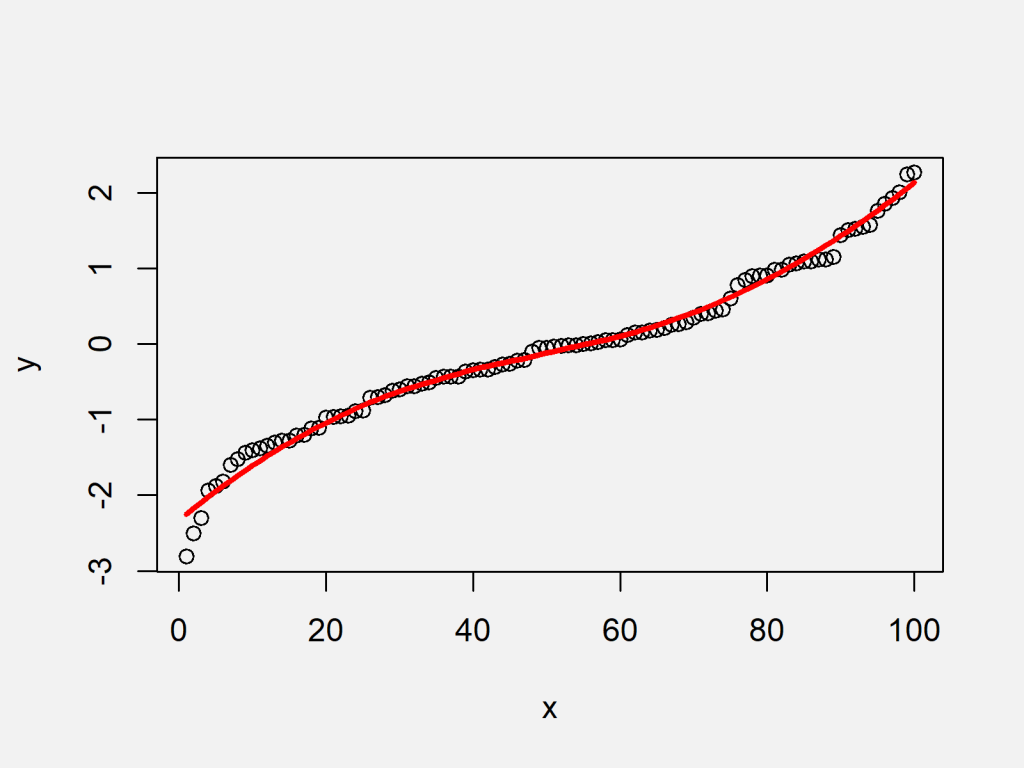
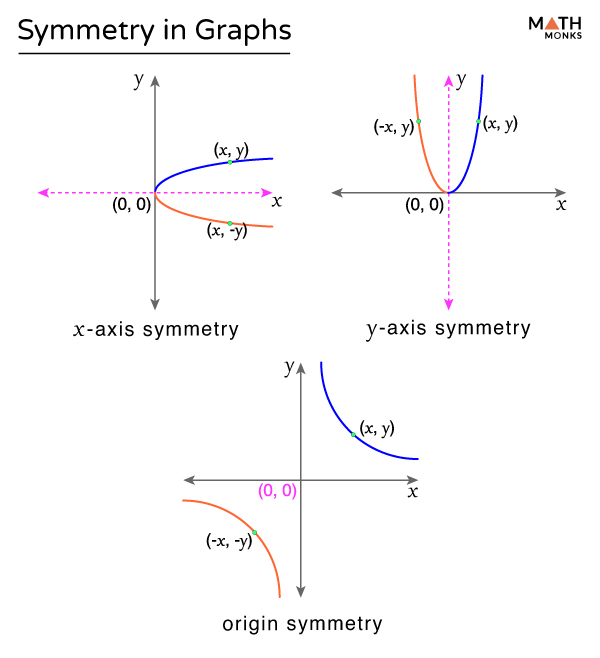
The turning points of a smooth graph must always occur at rounded curves. A smooth curve is a graph that has no sharp corners. It is a curve in the real plane parametrized f:

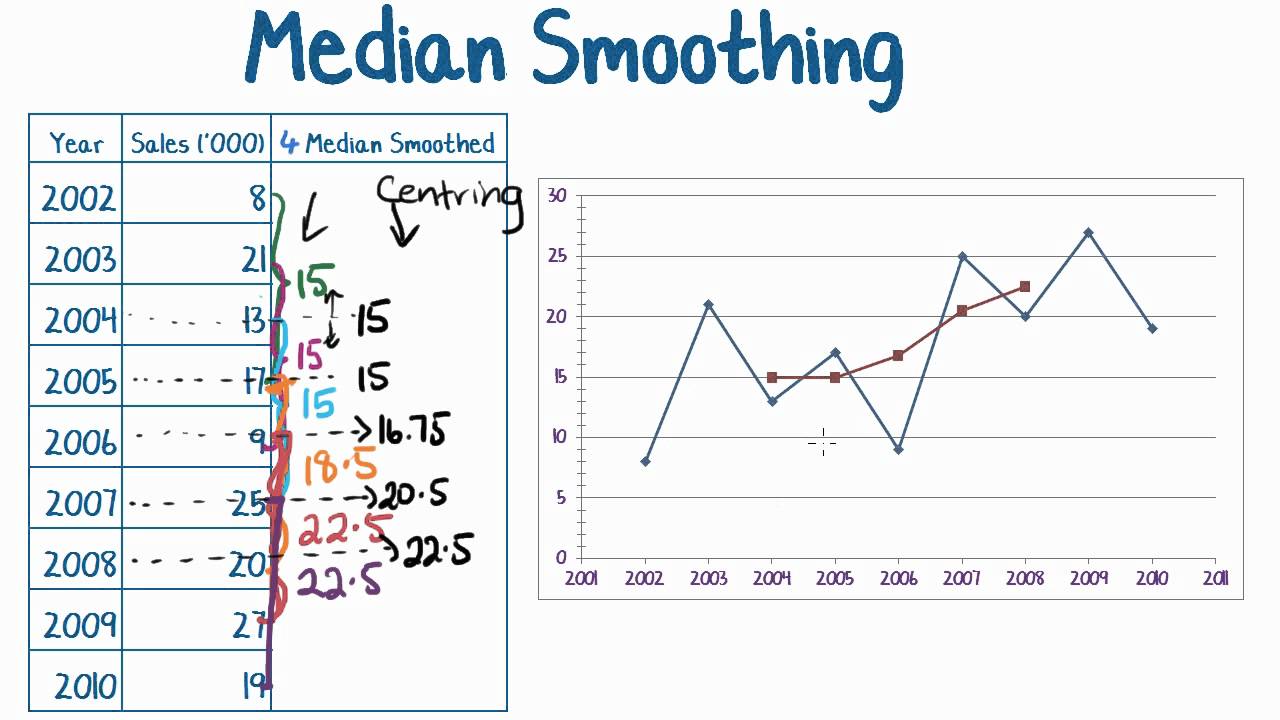
This is a very simple kind of filtering (box filtering in frequency domain), so you can try gently attenuating high order frequencies if the distortion is unacceptable. Smoothing is not a method of data analysis, but is purely a way to create a more attractive graph. It is the zero set x3 = y2 x 3 = y 2.

A smooth function must be differentiable, and the derivative must be continuous. A continuous function has no breaks in its graph: Thanks to all of you who support me on.