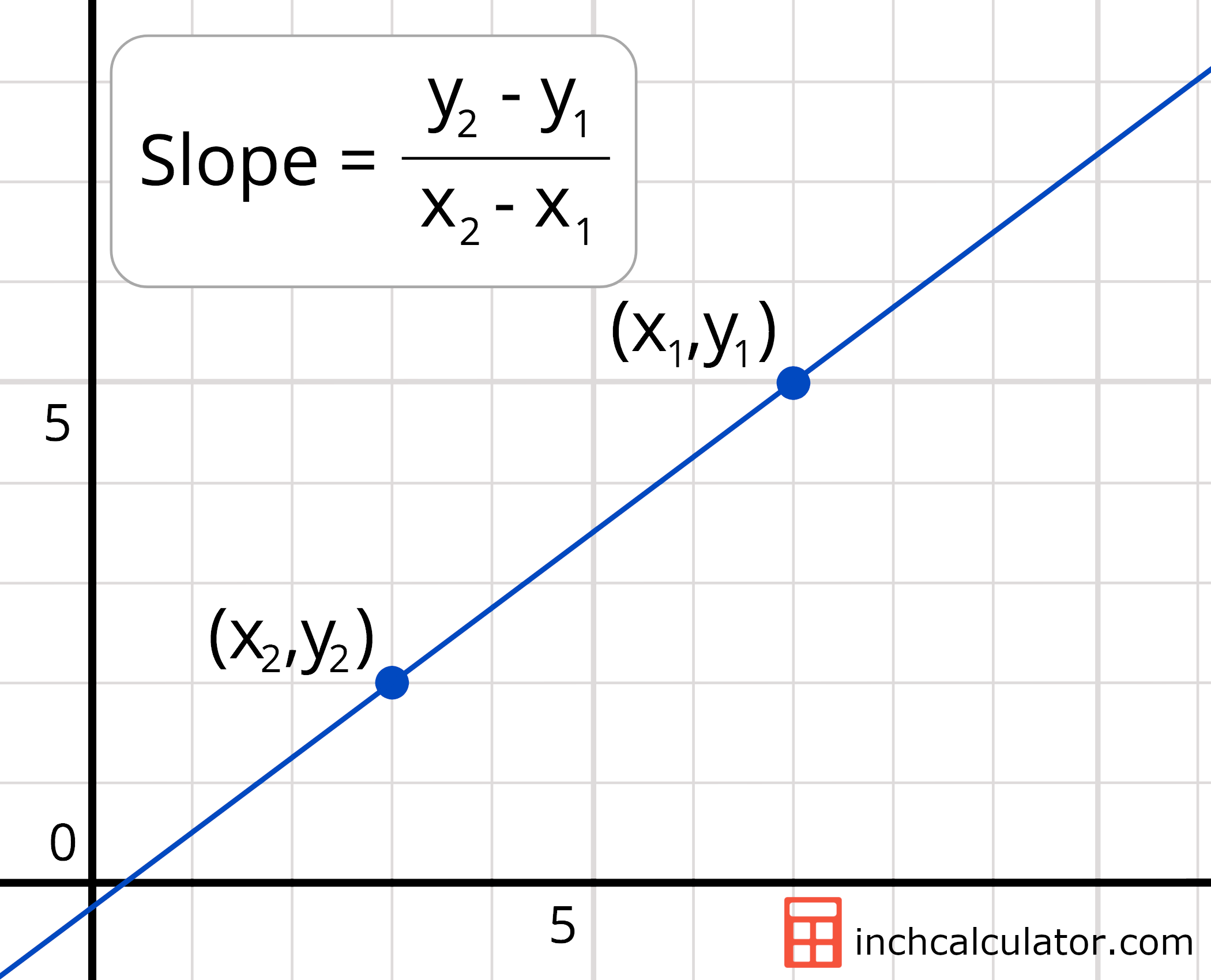Glory Tips About Does A Curved Line Have Slope Time Series Graph Python

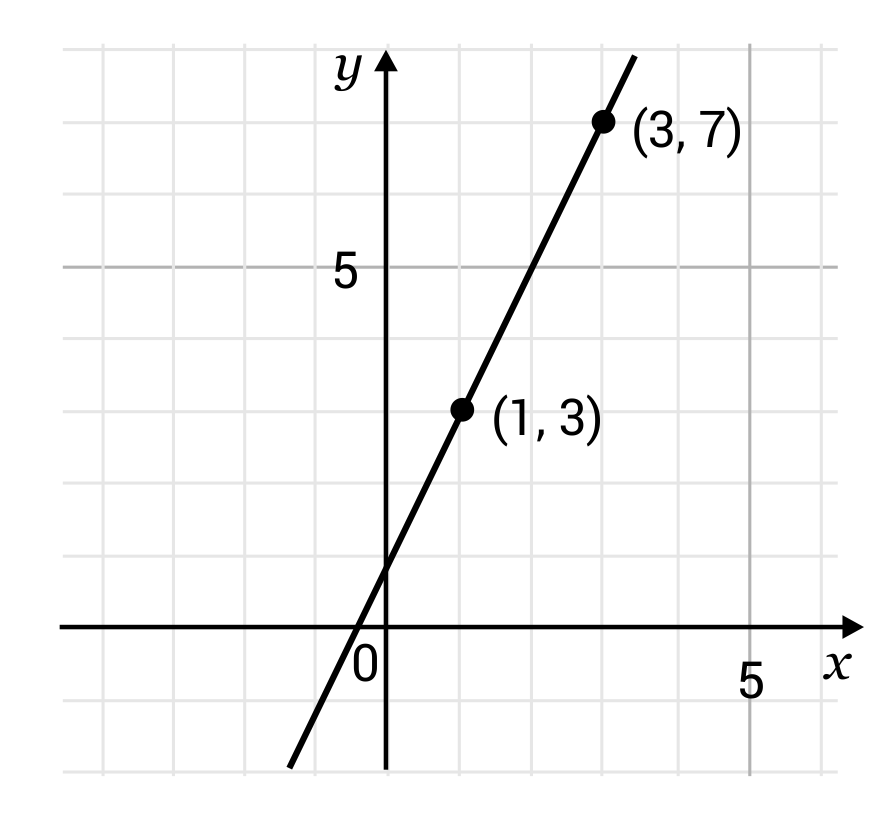
The steeper it is, the bigger the slope.

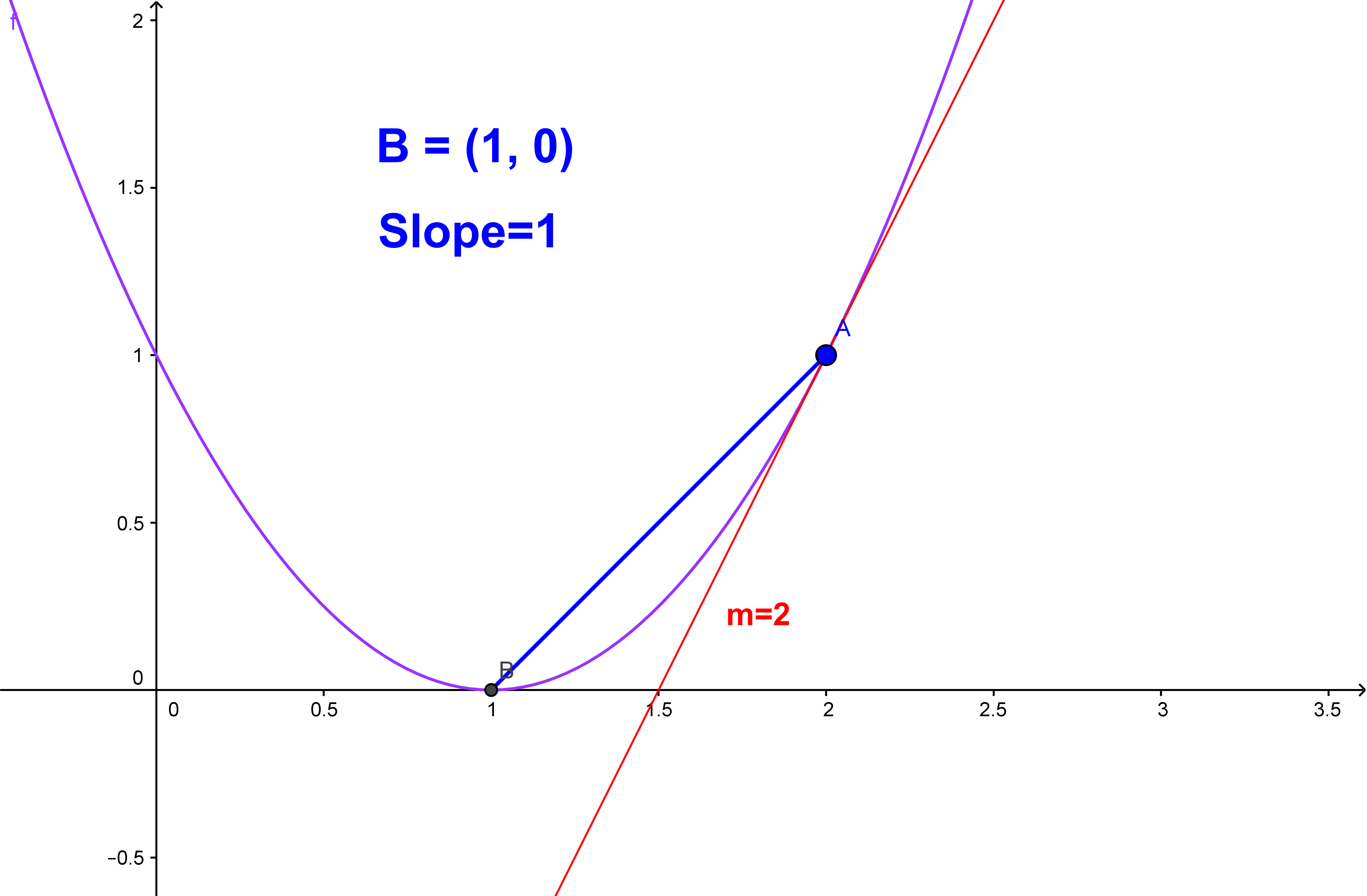
Does a curved line have a slope. Learn how to write the slope formula from scratch and how to apply it to find the slope of a line from two points. The top diagram at the right is the graph of y = 2 x and the slope of this graph at the point (0,1) is the slope of the tangent line at (0,1). But finding the slope of the straight line that joins p and q just requires the formula you quoted.

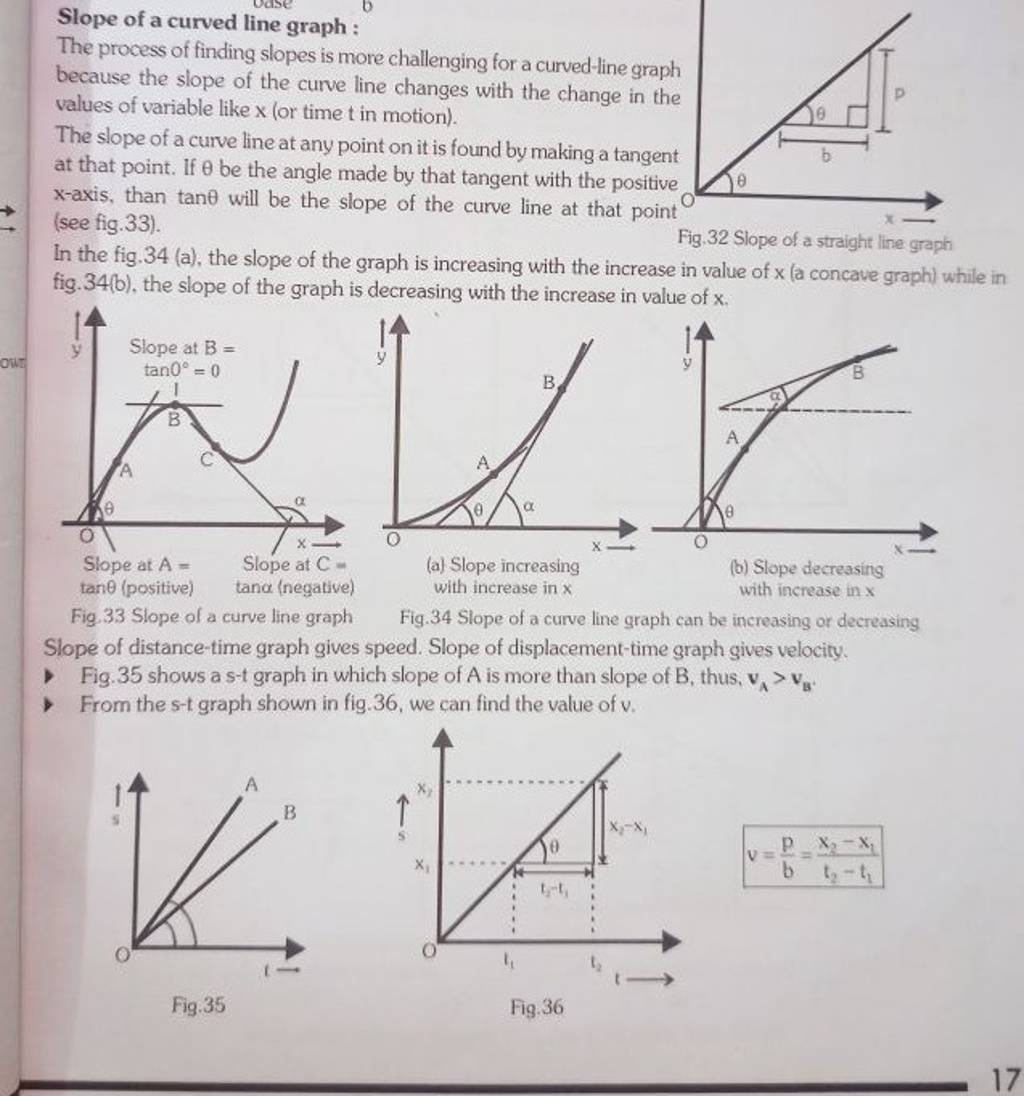
What is the slope of the line on the geoboard in figure \(\pageindex{4}\)? A straight line maintains a constant slope, while a curved line has a varying slope. Calculation of this requires some concepts from the calculus.

Find the slope from two points. A curved line is a type of line that is not straight and is bent. Types of slopes of a line.

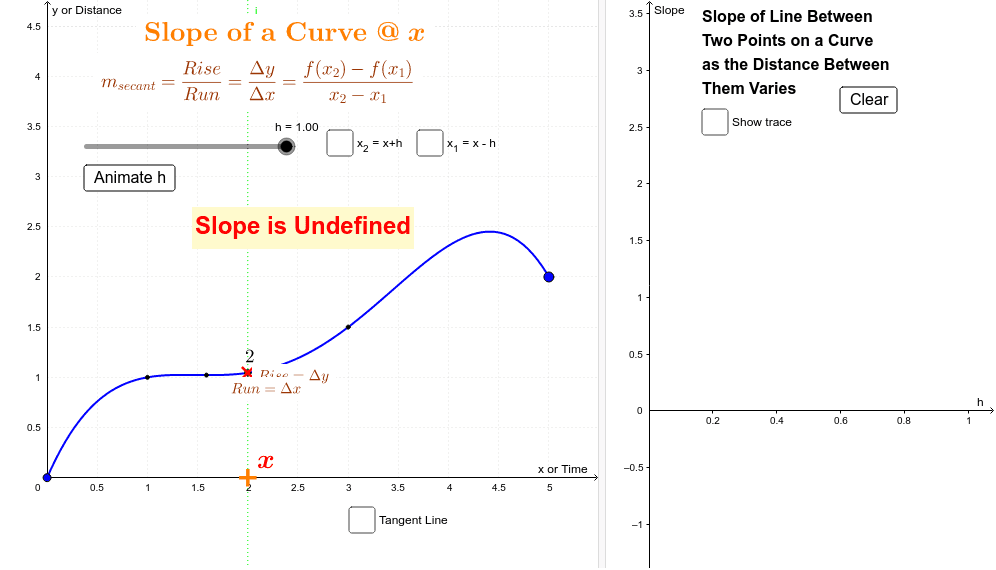
The slope of a smooth curve at a pont on the curve is defined as the slope of the tangent line at that point. You can determine the slope of a line from its graph by looking at the rise and run. It is continuous and smooth, without any sharp turns.

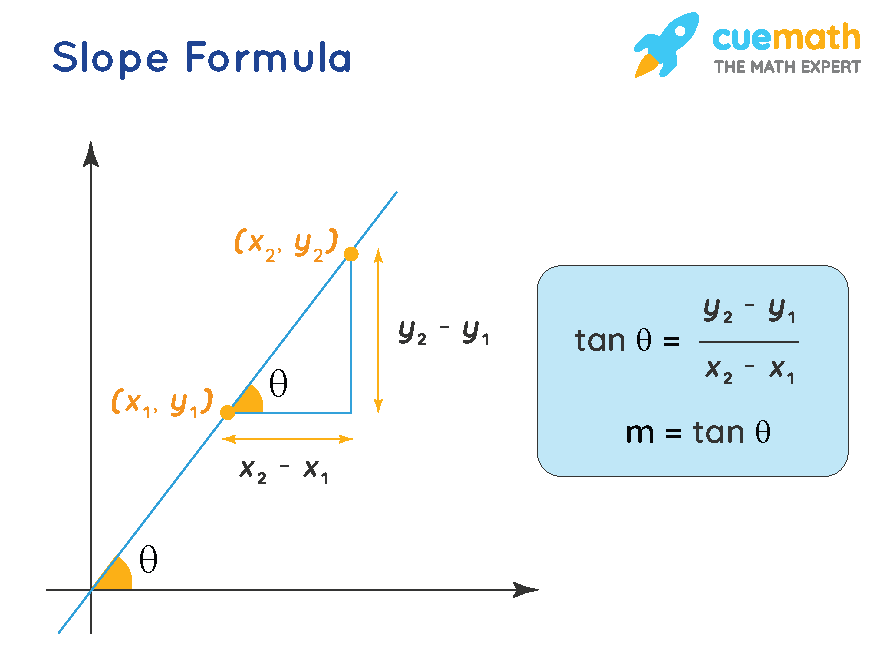
Slope of a line. In this section, we will explore the concepts of slope. The slope of a line is defined as a fraction:

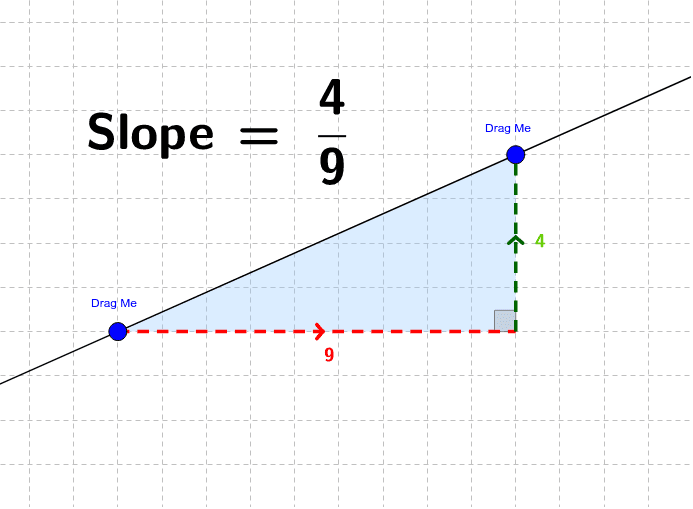
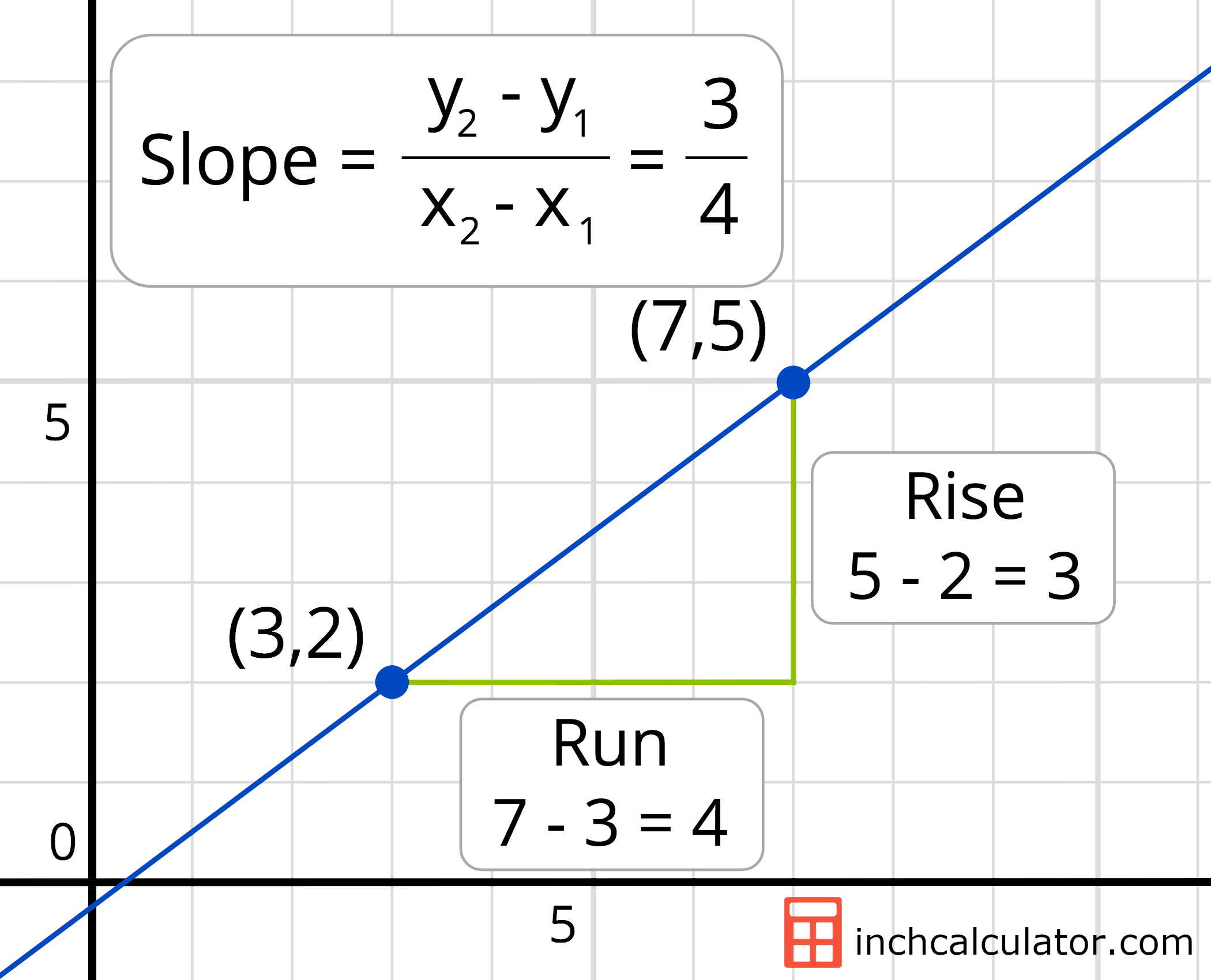
The vertical change between two points is called the rise, and the horizontal change is called the run. The word “slope” in math has roughly the same meaning in math as it has in everyday language: When the curve is approximated by a series of points, the slope of the curve may be approximated by the slope of.

Find the slope with algebra. Distinguish between graphs of lines with negative and positive slopes. The same applies to a curve.

When we say the slope of a curve, we mean the slope of tangent to the curve at a point. Generalizing this, differential calculus defines the slope of a curve at a point as the slope of its tangent line at that point. If a line goes down as you move to the right, it has a negative slope.

The rise measures the vertical change and the run measures the horizontal change when moving from one point on the line to another on the line. According to definition the slope of a curve at a point is equal to the slope of tangent at that point. Since tangent is a straight line why not just find the tan of the angle of inclination of the straight line which would give us the slope of the line and eventually the slope of the curve at that point.

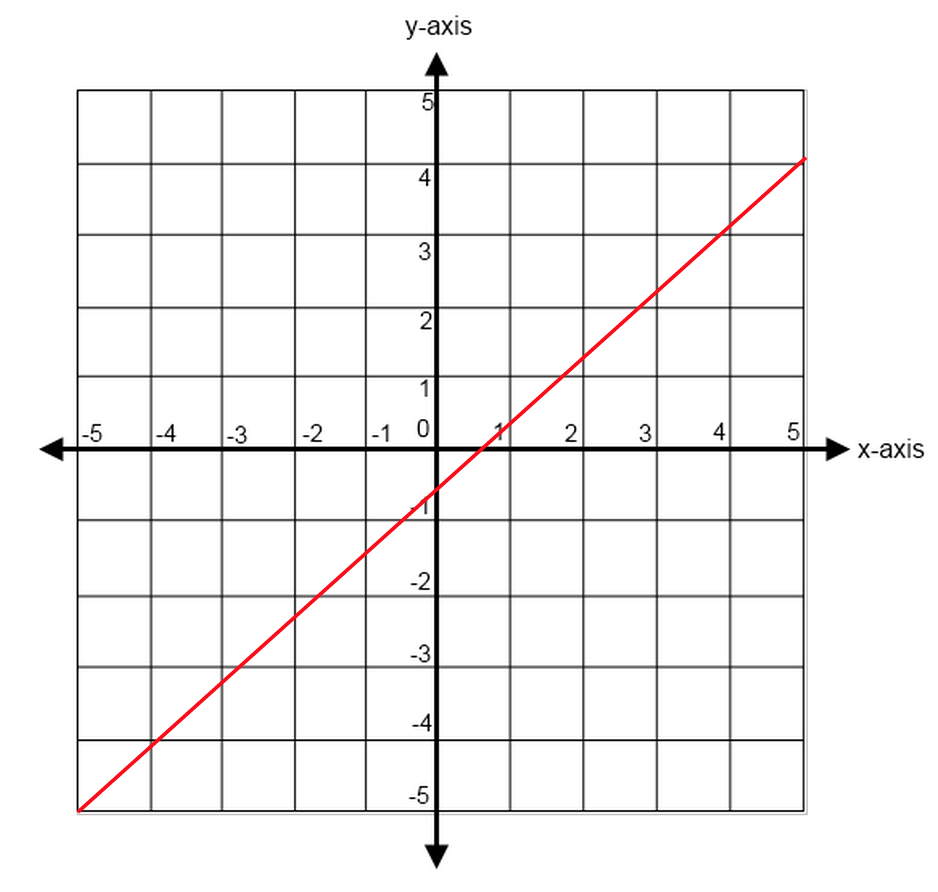
So if we get close enough, we might as well get to those two points where a curve becomes a line, and that line would have exactly the same slope as the tangent line. Even if you get a number like 5 as a slope, you need to change it into 5/1 (fraction form) to understand what it means related to the lines movement. The slope (also called gradient) of a line shows how steep it is.