Can’t-Miss Takeaways Of Tips About Can A Curved Graph Have Slope How To Create Trend In Excel

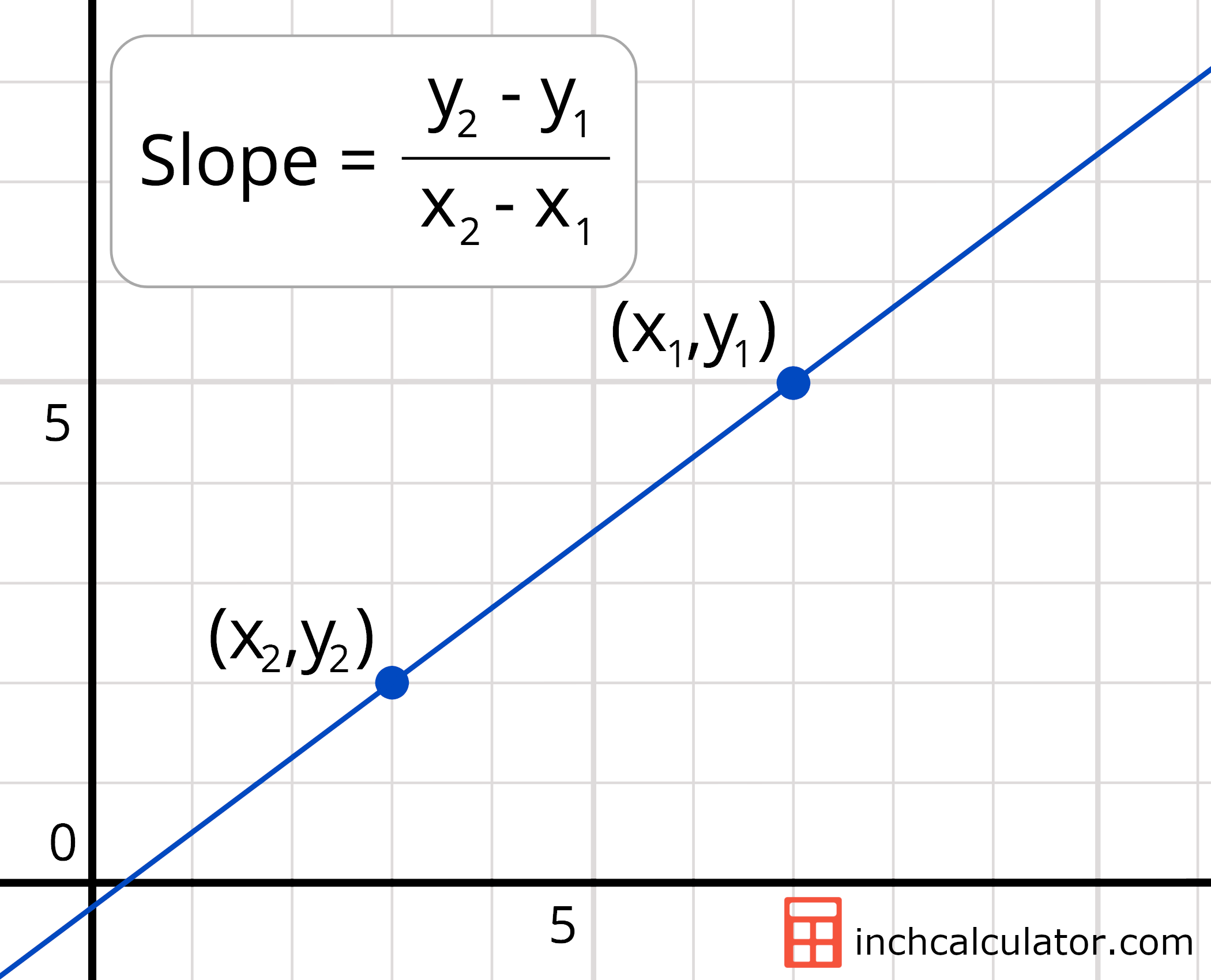
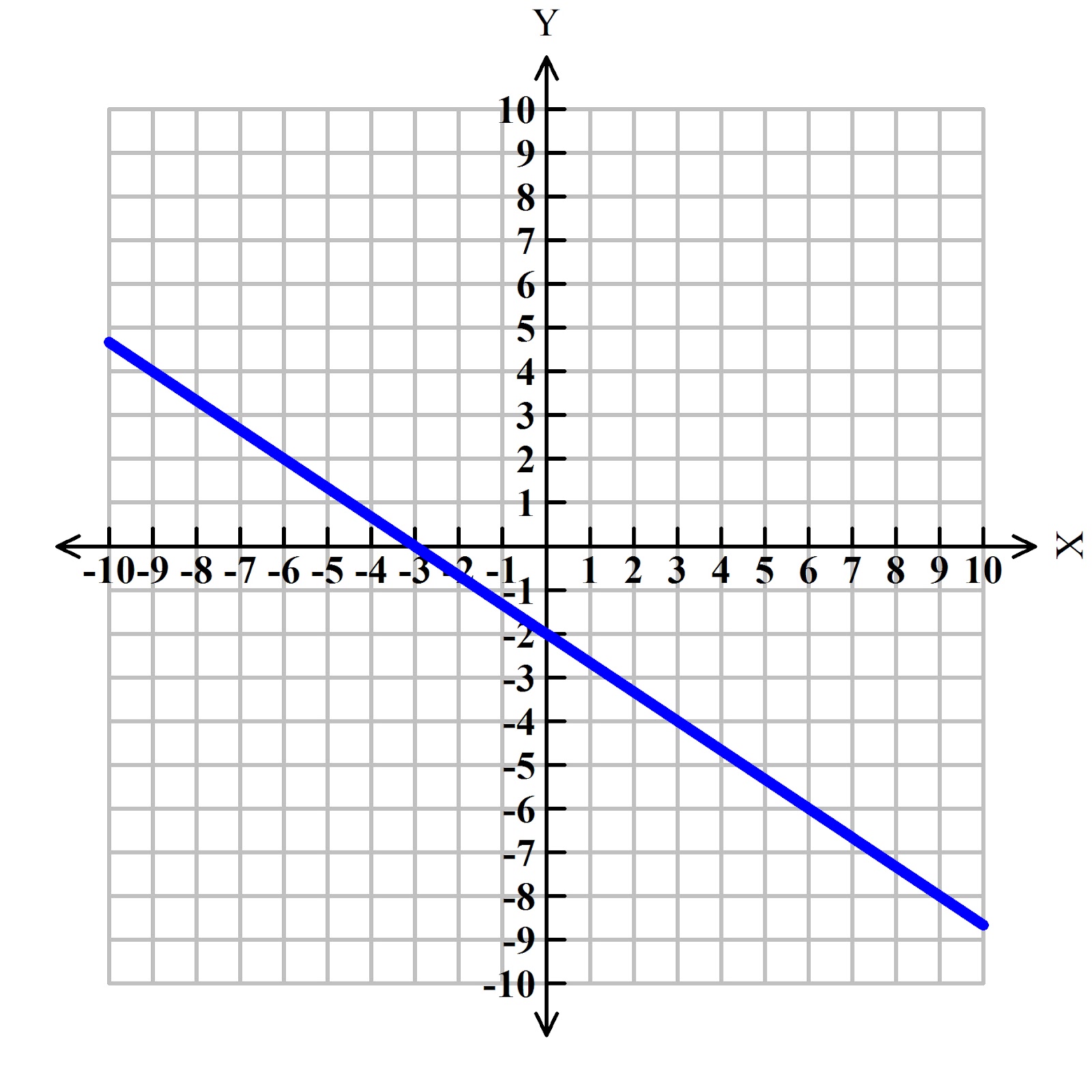
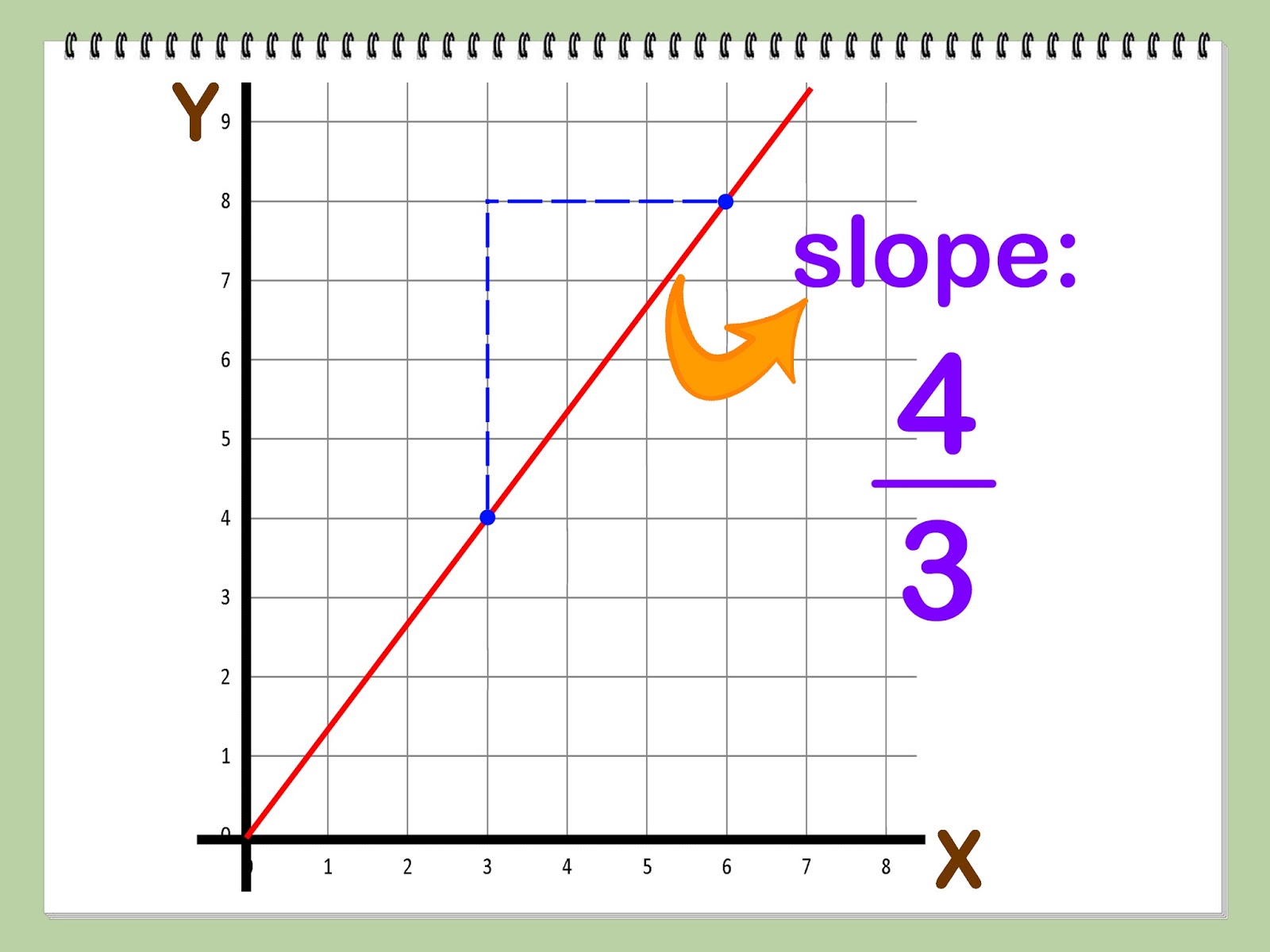
Use \(m = \frac{\text{rise}}{\text{run}}\) to find the slope of a line from its graph;

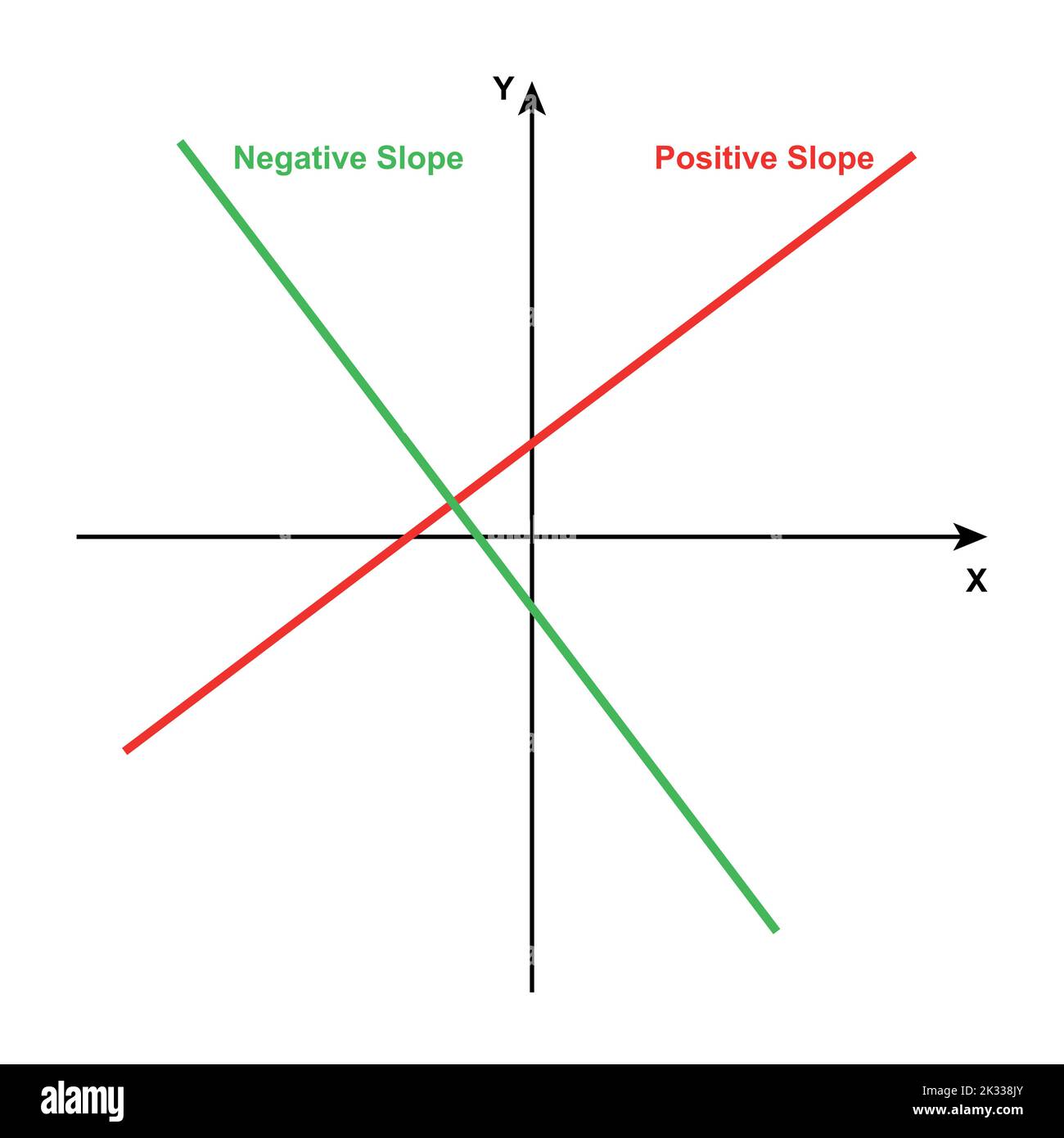
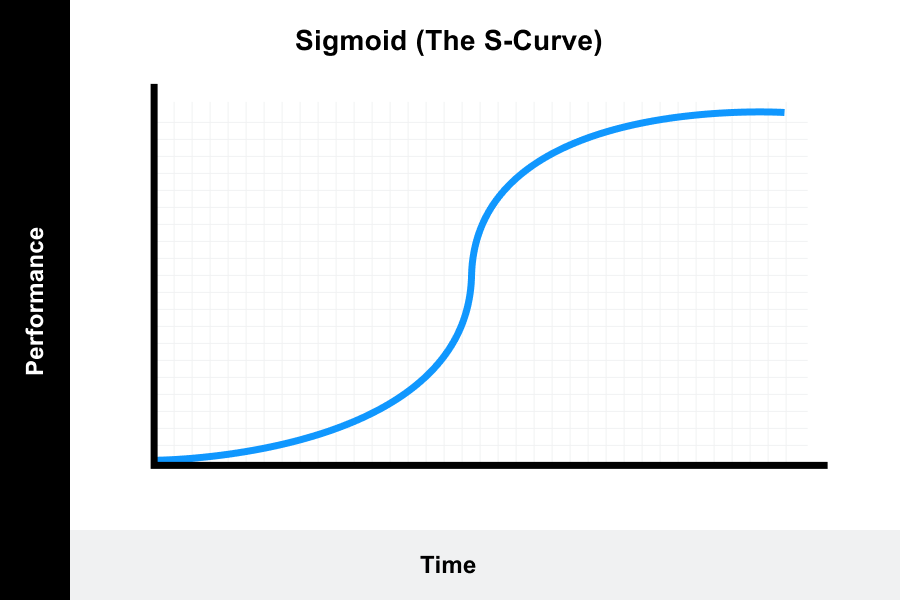
Can a curved graph have a slope. Find the slope of horizontal and vertical lines; The concept of slope really applies to straight lines. Calculation of this requires some concepts from the calculus.

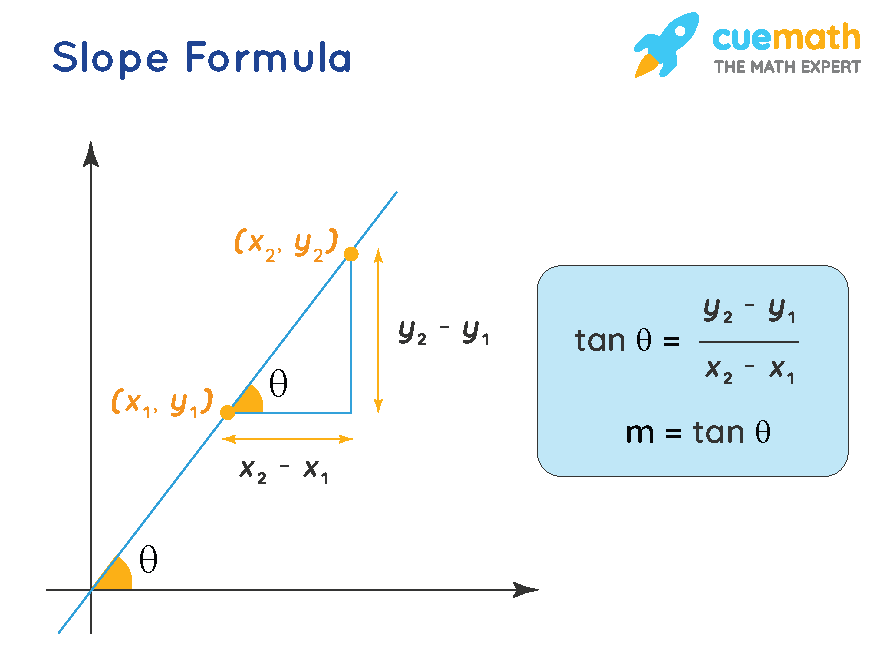
If the given curve is \(y=f(x),\) we evaluate \(\dfrac { dy }{ dx } \) or \(f'(x)\) and substitute the value of \(x\) to find the slope. For a line of the form (or any other form) \(y=mx+c,\) we can find its slope by simply taking any two values of \(x,\) \({x}_{1}\) and \({x}_{2},\) and their respective \( y\) values, \({y}_{1}\) and \({y}_{2}\). Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

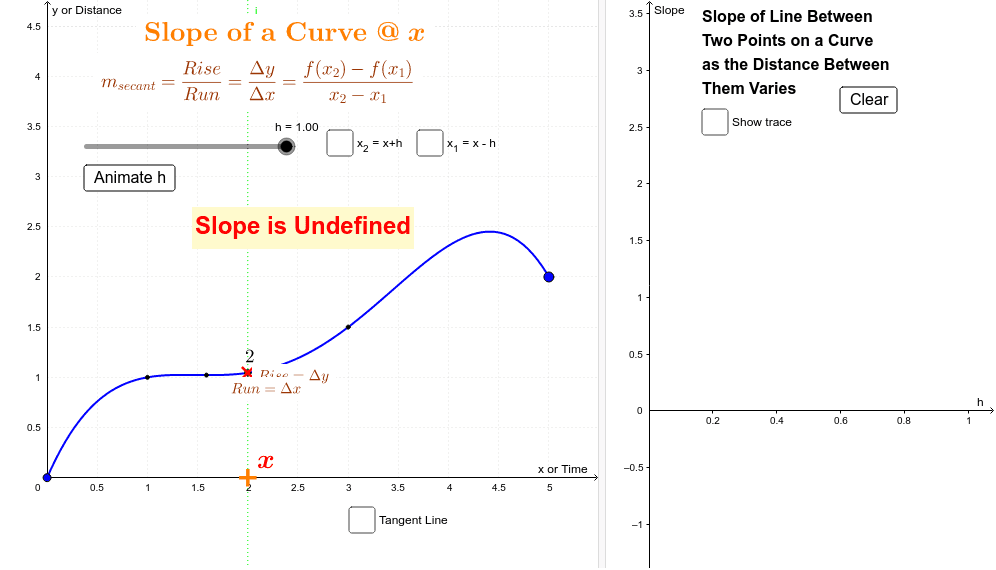
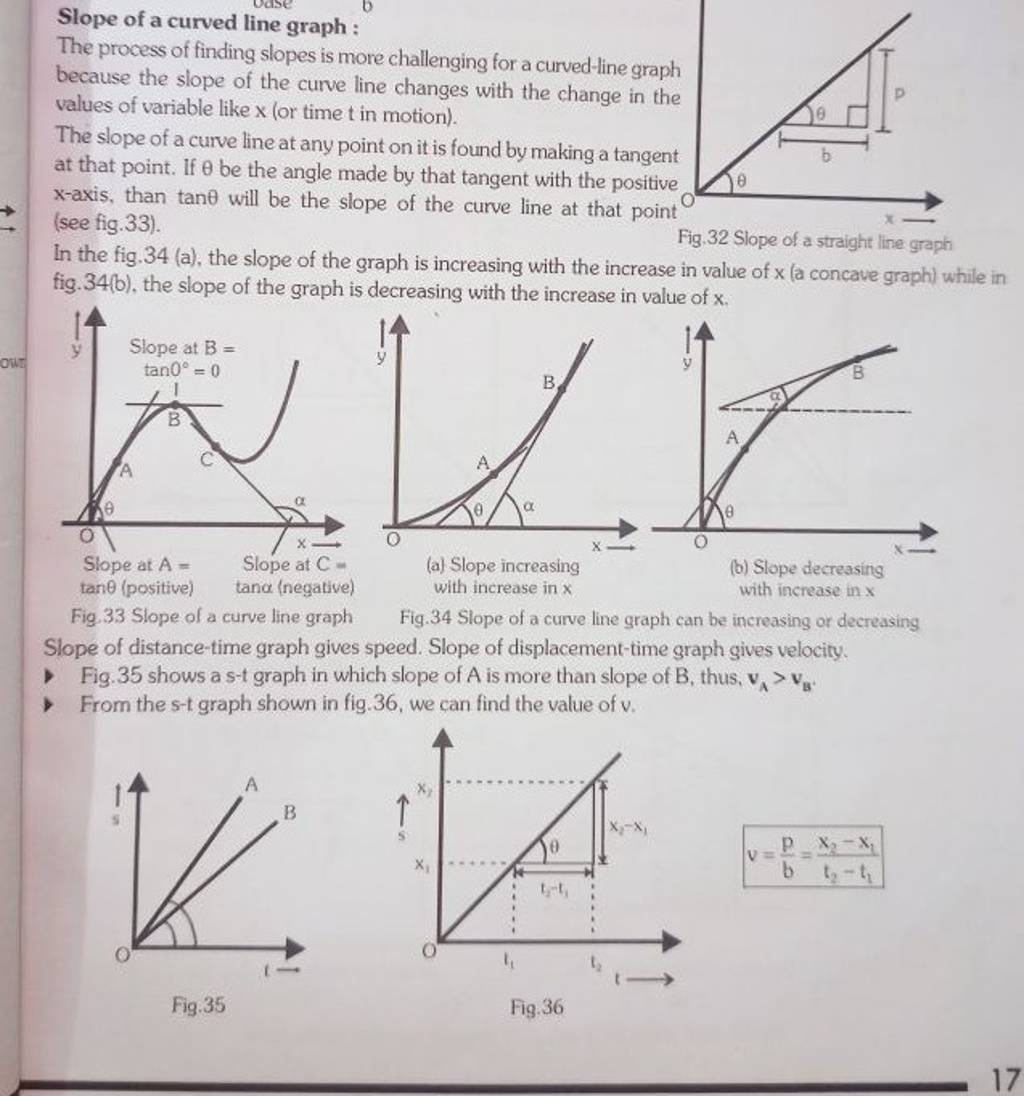
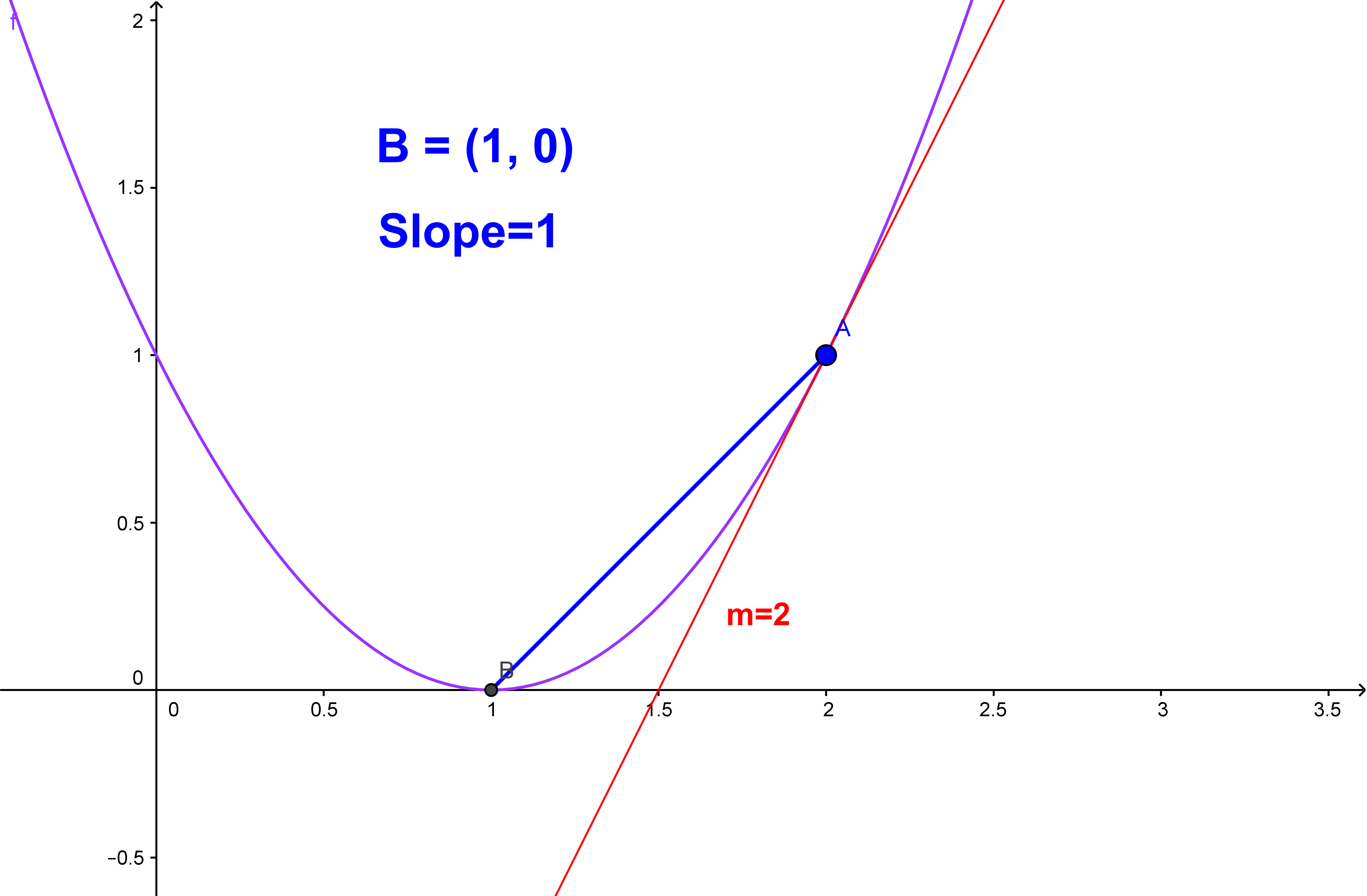
It does not have a slope per se, it only has an instantaneous slope at a given point (a line that is tangent to the point on the curve). Calculate the slope of your best fit line (with units) by selecting two points from the best fit line. The slope of a curve is a slope of a tangent line for a curve at one point.

You can determine the slope of a line from its graph by looking at the rise and run. Explore math with our beautiful, free online graphing calculator. The slope of a curve at a point is equal to the slope of the tangent line at that point.

In other words, for every three units we move vertically down the line, we move four units horizontally to the right. If you have sleep saved as a favorite, you can access it from the summary page in the health app. The bar graph by default is set to d for daily.

One characteristic of a line is that its slope is constant all the way along it. Pick two points that are reasonably spaced (one near the beginning of the line and one near the end). Find the derivative (dy/dx) of the function y = f(x).

It is also defined as the instantaneous change occurs in the graph with the very minor increment of x. A tangent line can identify the slope of a curved line at one point. Time graph, the tangent line indicates the instantaneous velocity.

So if we get close enough, we might as well get to those two points where a curve becomes a line, and that line would have exactly the same slope as the tangent line. So, you can choose any 2 points along the graph of the line. This can help you find sooooo many stuff like the instantaneous velocity, etc, etc,!, using integral calculus (closely inked to differential calculus), you can find the area under a graph and understand why and what that area provides!

We're given the graph of a line and asked to find its slope. When dealing with a curved line, where the slope is changing, you can’t use the same formula. The curvature, on the other hand, is the inverse of the radius of the circle that best approximates the curve at that point, a.k.a.

But enough about theory, let’s take a look at how we can actually find slope of a curve (or slope of a tangent of a curve). Formula for slope of a curve. But finding the slope of the straight line that joins p and q just requires the formula you quoted.